Cho hàm số y=(m-1)x+2m-5 (d1)
a. Tính giá trị của m để đg thẳng d1 song song bs đg thẳng y=3x+1 d2
b. Vs giá trị nào của m thì dg thẳng d1 và d2 cắt nhau tại 1 điểm trên trục hoành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 12 2018
a)
đường thẳng (d1) song song với đường thẳng (d2) khi :
a = a' và b khác b'
suy ra :
\(m-1=3\) \(\Leftrightarrow m=4\)
vậy đường thẳng (d1) song song với đường thẳng (d2) khi m = 4
23 tháng 12 2023
a: Để hàm số y=(m-1)x+3 đồng biến trên R thì m-1>0
=>m>1
Để hàm số y=(m-1)x+3 nghịch biến trên R thì m-1<0
=>m<1
b: Thay m=3 vào (d), ta được:
\(y=\left(3-1\right)x+3=2x+3\)
Vẽ đồ thị:
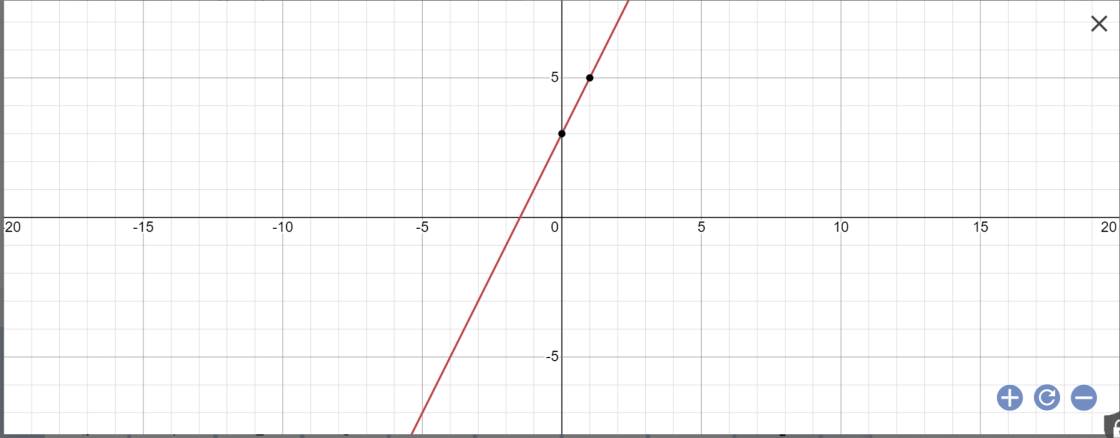
c: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=2\\3\ne-1\left(đúng\right)\end{matrix}\right.\)
=>m-1=2
=>m=3
d: Thay x=-2 và y=0 vào (d1), ta được:
\(-2\left(m-1\right)+3=0\)
=>-2(m-1)=-3
=>\(m-1=\dfrac{3}{2}\)
=>\(m=\dfrac{3}{2}+1=\dfrac{5}{2}\)
CH
Cô Hoàng Huyền
Admin
VIP
21 tháng 11 2017
Bài 1)
a) Xét phương trình hoành độ giao điểm: \(2x+3+m=3x+5-m\)
\(\Leftrightarrow x=3+m+m-5\Leftrightarrow x=2m-2\)
Để giao điểm của hai đường thẳng trên nằm trên trục tung thì \(2m-2=0\Leftrightarrow m=1\)
b) Do (d) // (d') nên (d) có phương trình \(y=-\frac{1}{2}x+b\)
Do (d) cắt trục hoành tại điểm có hoành độ x = 10 nên điểm (10;0) thuộc đường thẳng (d0.
Vậy thì \(0=-\frac{1}{2}.10+b\Leftrightarrow b=5\)
Vậy phương trình đường thẳng (d) là \(y=-\frac{1}{2}x+5\)
Bài 2)
a) Để (d1)//(d2) thì \(4m=3m+1\Leftrightarrow m=1\)
b) Để (d1)//(d2) thì \(4m\ne3m+1\Leftrightarrow m\ne1\)
Khi m = 2, ta có phương trình hoành độ giao điểm là:
\(8x-7=7x-7\Leftrightarrow x=0\)
Với \(x=0,y=-7\)
Vậy tọa độ giao điểm của (d1) và (d2) là (0; -7)
2 tháng 1 2023
a: Thay x=-2 và y=-2 vào (d1), ta đc:
-2(2m+1)+m-3=-2
=>-4m-2+m-3=-2
=>-3m-5=-2
=>-3m=3
=>m=-1
b: Tọa độ giao của (d2) với trục hoành là:
y=0 và (2a+1)x+4a-3=0
=>x=-4a+3/2a+1
Để x nguyên thì -4a-2+5 chia hết cho 2a+1
=>\(2a+1\in\left\{1;-1;5;-5\right\}\)
=>\(a\in\left\{0;-1;2;-3\right\}\)
CM
26 tháng 6 2019
b) d 1 cắt trục hoành tại điểm có hoành độ bằng – 3 khi:
0 = -3m + 2m - 1 ⇔ -m - 1 = 0 ⇔ m = -1
Vậy với m = -1 thì d 1 cắt trục hoành tại điểm có hoành độ bằng – 3
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2019
a/ Để (d1) song song (d2)
\(\Leftrightarrow\left\{{}\begin{matrix}m-1=3\\2m-5\ne1\end{matrix}\right.\) \(\Rightarrow m=4\)
b/ Giao điểm A của (d2) và trục hoành:
\(y=0\Rightarrow3x+1=0\Rightarrow x=-\frac{1}{3}\Rightarrow A\left(-\frac{1}{3};0\right)\)
Để (d1) và (d2) cắt nhau trên trục hoành \(\Leftrightarrow\) (d1) đi qua A
\(\Leftrightarrow-\frac{1}{3}\left(m-1\right)+2m-5=0\Rightarrow m=\frac{14}{5}\)
4 tháng 6 2022
a: Để (d1)//(d2) thì m-1=3
hay m=4
b:
Thay y=0 vào y=3x+1, ta được:
3x+1=0
hay x=-1/3
Để (d1) và (d2) cắt nhau tại một điểm trên trục hoành thì (d1) đi qua (-1/3;0)
Thay x=-1/3 và y=0 vào (d1), ta được:
\(-\dfrac{1}{3}\left(m-1\right)+2m-5=0\)
=>-1/3m+1/3+2m-5=0
=>5/3m-14/3=0
=>5/3m=14/3
hay m=14/5
CM
21 tháng 4 2019
a) Để d1 trùng d2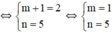 
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2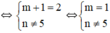 
Vậy m = 1, n ≠ 5.
a/ \(\left\{{}\begin{matrix}m-1=3\\2m-5\ne1\end{matrix}\right.\) \(\Rightarrow m=4\)
b/ Giao điểm A của (d2) và trục hoành: \(\left\{{}\begin{matrix}y=0\\3x+1=0\end{matrix}\right.\) \(\Rightarrow A\left(-\frac{1}{3};0\right)\)
Để (d1) qua A \(\Rightarrow-\frac{1}{3}\left(m-1\right)+2m-5=0\Rightarrow m=\frac{14}{5}\)