tìm m để pt x3-3x2-mx=0 có 3 nghiệm pb. trong đó có đúng 2 nghiệm dương
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Em có x 3 − 3 x 2 − m = 0 ⇔ x 3 − 3 x 2 = m
Khi đó yêu cầu đầu bài tương đương với đồ thị hàm số y = x 3 − 3 x 2 cắt đường thẳng y = m tại 3 điểm trong đó có 2 điểm có hoành độ lớn hơn 1. Em có đồ thị hàm số y = x 3 − 3 x 2 như hình bên.
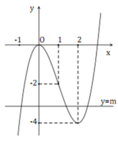
Từ đồ thị em thấy − 4 < m < − 2

Đáp án A
Ghi nhớ: Nếu hàm số ![]()
liên tục trên đoạn ![]() và
và ![]() thì phương trình
thì phương trình ![]()
có ít nhất một nghiệm nằm trong khoảng ![]() .
.

Đáp án D
· Điều kiện cần:
Giả sử phương trình đã cho có 3 nghiệm phân biệt x 1 ; x 2 ; x 3 lập thành một cấp số cộng
Khi đó: x 1 + x 3 = 2 x 2 x 1 + x 2 + x 3 = 3 ⇔ 3 x 2 = 3 ⇔ x 2 = 1 .
Với x 2 = 1 thay vào phương trình ta được:
1 − 3 + m + 2 − m = 0 (luôn đúng).
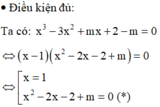
Phương trình đã cho có 3 nghiệm phân biệt tương đương với phương trình (*) có 2 nghiệm phân biệt khác 1.
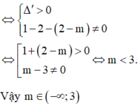

3.
Phương trình có 2 nghiệm khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta=m^2-12\left(m+1\right)\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne-1\\\left[{}\begin{matrix}m\ge6+4\sqrt{3}\\m\le6-4\sqrt{3}\end{matrix}\right.\end{matrix}\right.\) (1)
Khi đó theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{m}{m+1}\\x_1x_2=\dfrac{3}{m+1}\end{matrix}\right.\)
Hai nghiệm cùng lớn hơn -1 \(\Rightarrow-1< x_1\le x_2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1+1\right)\left(x_2+1\right)>0\\\dfrac{x_1+x_2}{2}>-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2+x_1+x_1+1>0\\x_1+x_2>-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{m+1}-\dfrac{m}{m+1}+1>0\\-\dfrac{m}{m+1}>-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{m+1}>0\\\dfrac{m+2}{m+1}>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>-1\\\left[{}\begin{matrix}m>-1\\m< -2\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m>-1\)
Kết hợp (1) \(\Rightarrow\left[{}\begin{matrix}-1< m< 6-4\sqrt{3}\\m\ge6+4\sqrt{3}\end{matrix}\right.\)
Những bài này đều là dạng toán lớp 10, thi lớp 9 chắc chắn sẽ không gặp phải
1. Có 2 cách giải:
C1: đặt \(f\left(x\right)=x^2+2mx-3m^2\)
\(x_1< 1< x_2\Leftrightarrow1.f\left(1\right)< 0\Leftrightarrow1+2m-3m^2< 0\Rightarrow\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\)
C2: \(\Delta'=4m^2\ge0\) nên pt luôn có 2 nghiệm
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=-3m^2\end{matrix}\right.\)
\(x_1< 1< x_2\Leftrightarrow\left(x_1-1\right)\left(x_2-1\right)< 0\)
\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1< 0\)
\(\Leftrightarrow-3m^2+2m+1< 0\Rightarrow\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\)
\(x\left(x^2-3x-m\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-3x-m=0\left(1\right)\end{matrix}\right.\)
Để pt đã cho có 3 nghiệm pb trong đó có 2 nghiệm dương \(\Leftrightarrow\) (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4m+9>0\\3>0\\-m>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-\frac{9}{4}\\m< 0\end{matrix}\right.\)
\(\Rightarrow-\frac{9}{4}< m< 0\)