Gieo một đồng xu 4 lần . Mô tả không gian mẫu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 10 2017
a. Mỗi phần tử của không gian mẫu chỉ rõ ba đồng tiền xuất hiện ngẫu nhiên mặt sấp hay mặt ngửa. Vì vậy cần chọn phương án C
CM
12 tháng 8 2018
Kí hiệu mặt sấp là S, mặt ngửa là N.
Ω = S ; N S ; N N S ; N N N S ; N N N N S ; NNNNN ⇒ Ω = 6.
CM
16 tháng 5 2017
a. Không gian mẫu của phép thử gồm 5 phần tử được mô tả sau:
Ω = {S, NS, NNS, NNNS, NNNN}
b. Xác định các biến cố:
+ A: "Số lần gieo không vượt quá 3"
A = {S, NS, NNS}
+ B: "Số lần gieo là 4"
B = {NNNS, NNNN}.
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây
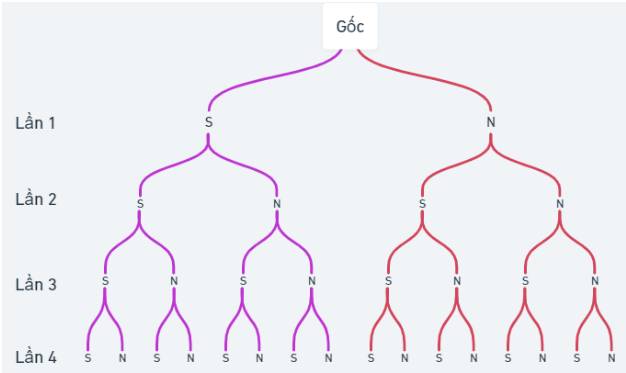
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).
Y
30 tháng 4 2023
Không gian mẫu \(\Omega=\left\{S;N;1;2;3;4;5;6\right\}\)
\(\Rightarrow n\left(\Omega\right)=8\)
\(A=\left\{S;2;4;6\right\}\)
\(\Rightarrow n\left(A\right)=4\)
Xác suất của biến cố \(A\) :
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4}{8}=\dfrac{1}{2}\)
LT
3 tháng 4 2017
a) Không gian mẫu của phép thử đã cho là:
Ω = {S, NS, NNS, NNNS, NNNN}.
b) A = {S, NS, NNS};
B = {NNNS, NNNN}.
NN
0
CM
6 tháng 1 2019
a. Không gian mẫu gồm 36 kết quả đồng khả năng xuất hiện, được mô tả như sau:
Ta có: Ω = {(i, j) | 1 ≤ i , j ≤ 6}, trong đó i, j lần lượt là số chấm xuất hiện trong lần gieo thứ nhất và thứ hai, n(Ω) = 36.
b. A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} ⇒ n(A) = 6
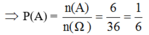
B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}
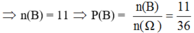
giúp mình với
Không gian (KG) mẫu: gồm 8 phần tử
Ω = {SSS, SSN, SNS, SNN, NSS, NSN, NNS, NNN}.
Trong đó SSS là kết quả "ba lần gieo đồng tiền xuất hiện mặt sấp"; NSS là kết quả "lần đầu đồng tiền xuất hiện mặt ngửa, lần thứ 2, lần thứ 3 xuất hiện mặt sấp"
bn k mk nha