10n2+n-10 ⋮ n-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2023
=>3n^3+n^2+9n^2-1-4 chia hết cho 3n+1
=>\(3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-1;1\right\}\)
CM
22 tháng 5 2019
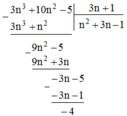
Ta có: 3 n 3 + 10 n 2 - 5 = 3 n + 1 n 2 + 3 n - 1 - 4
Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)
3n + 1 ∈ {-4; -2; -1; 1; 2; 4}
3n + 1 = -4⇒ 3n = -5⇒ n =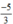 
∉ Z : loại
3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z
3n + 1 = -1⇒ 3n = -2⇒ n =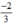 
∉ Z : loại
3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z
3n + 1 = 2⇒ 3n = 2⇒ n =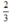 
∉ Z : loại
3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z
Vậy n ∈ {-1; 0; 1} thì 3 n 3 + 10 n 2 - 5 chia hết cho 3n + 1.
XU
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
Đặt \(A=n^4-10n^2+9\)
\(n^4-n^2-9\left(n^2-1\right)=n.n\left(n-1\right)\left(n+1\right)-9\left(n^2-1\right)\)
Do \(n\left(n-1\right)\left(n+1\right)\) là tích 3 số nguyên liên tiếp nên luôn chia hết cho 3
\(\Rightarrow A⋮3\)
Lại có: \(A=\left(n^2-1\right)\left(n^2-9\right)=\left(n-1\right)\left(n+1\right)\left(n-3\right)\left(n+3\right)\)
Do n lẻ, đặt \(n=2k+1\)
\(\Rightarrow A=\left(2k+1-1\right)\left(2k+1+1\right)\left(2k+1-3\right)\left(2k+1+3\right)\)
\(=2k\left(2k+2\right)\left(2k-2\right)\left(2k+4\right)\)
\(=16k\left(k-1\right)\left(k+1\right)\left(k+2\right)\)
Do \(k\left(k-1\right)\left(k+1\right)\left(k+2\right)\) là tích 4 số nguyên liên tiếp nên luôn chia hết cho 8
\(\Rightarrow A⋮\left(16.8\right)\Rightarrow A⋮128\)
Mà 3 và 128 nguyên tố cùng nhau \(\Rightarrow A⋮\left(128.3\right)\Rightarrow A⋮384\)
26 tháng 12 2021
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
16 tháng 3 2021
1: Phân tích thành nhân tử
c) Ta có: \(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)
PT
1
20 tháng 10 2022
Bài4:
=>x(x^2+1)=0
>x=0
Bài 5:
=>\(3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
=>\(3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-\dfrac{2}{3};\dfrac{1}{3};-1;1;-\dfrac{5}{3}\right\}\)
25 tháng 10 2022
Bài 4:
x^3+x=0
=>x(x^2+1)=0
=>x=0
Bài 5:
\(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2-1-4⋮3n+1\)
=>\(3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-\dfrac{2}{3};\dfrac{1}{3};-1;1;-\dfrac{5}{3}\right\}\)
DD
0