tìm hệ số của x10 trong khai triển (1+x+x2)10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: SHTQ là: \(C^k_{10}\cdot x^{10-k}\cdot\left(\dfrac{2}{x}\right)^k=C^k_{10}\cdot2^k\cdot x^{10-2k}\)
Số hạng ko chứa x tương ứng với 10-2k=0
=>k=5
=>SH đó là 8064
b: SHTQ là; \(C^k_6\cdot x^{6-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_6\cdot2^k\cdot x^{6-3k}\)
Số hạng ko chứa x tương ứng với 6-3k=0
=>k=2
=>Số hạng đó là 60
c: SHTQ là: \(C^k_5\cdot\left(3x^3\right)^{5-k}\cdot\left(-\dfrac{2}{x^2}\right)^k\)
\(=C^k_5\cdot3^{5-k}\cdot\left(-2\right)^k\cdot x^{15-5k}\)
SH chứa x^10 tương ứng với 15-5k=10
=>k=1
=>Hệ số là -810

Số hạng tổng quát trong khai triển \(\left(2x-\dfrac{1}{x}\right)^{13}\) là \(C^k_{13}\cdot\left(2x\right)^{13-k}\cdot\left(-\dfrac{1}{x}\right)^{13}\)
\(=C^k_{13}\cdot2^{13-k}\cdot x^{13-k}\cdot\dfrac{\left(-1\right)}{x^{13}}\)
\(=C^k_{13}\cdot\left(-1\right)\cdot2^{13-k}\cdot x^{-k}\)
Hệ số của x^10 sẽ tương ứng với -k=10
=>k=-10(loại)
=>Không có x10 trong khai triển này
Số hạng tổng quát trong khai triển thế này mới đúng chứ em:
\(C_{13}^k.\left(2x\right)^k.\left(-\dfrac{1}{x}\right)^{13-k}=C_{13}^k.2^k.x^k.\left(-1\right)^{13-k}.x^{x-13}=C_{13}^k.2^k.\left(-1\right)^{13-k}.x^{2k-13}\)
Mặc dù kết quả vẫn là ko tồn tại số hạng chứa \(x^{10}\) do \(2k-13=10\Rightarrow k=\dfrac{23}{2}\) ko phải số tự nhiên

Đáp án C.
Tổng hệ số của các hạng tử chứa x 9 là C 9 9 + C 10 9 = 11.

Chọn A
(
1
+
x
+
x
2
+
x
3
)
10
![]()
![]()
![]()
Ta có các cặp (k;m): 2k + m = 5
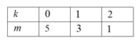
Suy ra hệ số của số hạng chứa
x
5
là: ![]()
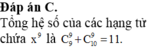
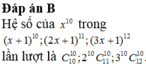
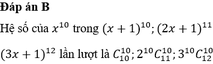

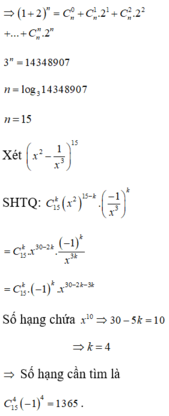
\(A=\left(1+x\left(1+x\right)\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^kx^k\left(1+x\right)^k=\sum\limits^{10}_{k=0}\left(\sum\limits^k_{i=0}C_{10}^kC_k^ix^{i+k}\right)\)
Do \(\left\{{}\begin{matrix}0\le i\le k\le10\\i+k=10\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(1;9\right);\left(2;8\right);\left(3;7\right);\left(4;6\right);\left(5;5\right)\)
Hệ số: \(C_{10}^9C_9^1+C_{10}^8C_8^2+C_{10}^7C_7^3+C_{10}^6C_6^4+C_{10}^5C_5^5\)
(i;k)=(0;10) nữa đc mà đk ạ