làm nhanh giúp mình vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
Diện tích xung quanh của hình hộp chữ nhật là:
\(\left(EH+CD\right)\cdot2\cdot EA=\left(8+6\right)\cdot2\cdot7=196\left(cm^2\right)\)
Thể tích của hình hộp chữ nhật là:
\(EA\cdot EH\cdot CD=7\cdot8\cdot6=336\left(cm^3\right)\)

1.
\(Ca+2H_2O\rightarrow Ca\left(OH\right)_2+H_2\)
\(2Na+2H_2O\rightarrow2NaOH+H_2\)
\(P_2O_5+3H_2O\rightarrow2H_3PO_4\)
\(K_2O+H_2O\rightarrow2KOH\)
\(SO_2+H_2O\rightarrow H_2SO_3\)
\(SO_3+H_2O\rightarrow H_2SO_4\)
2.
(1)\(2KMnO_4\rightarrow\left(t^o\right)K_2MnO_4+MnO_2+O_2\)
(2)\(2Cu+O_2\rightarrow\left(t^o\right)2CuO\)
(3)\(CuO+H_2\rightarrow\left(t^o\right)Cu+H_2O\)
(4)\(4Na+O_2\rightarrow\left(t^o\right)2Na_2O\)
(5)\(Na_2O+H_2O\rightarrow2NaOH\)
(6)\(S+O_2\rightarrow\left(t^o\right)SO_2\)
(7)\(SO_2+H_2O\rightarrow H_2SO_3\)
(1) 2KMnO4 --to--> K2MnO4 + MnO2 + O2
(2) 2Cu + O2 --to--> 2CuO
(3) CuO + CO --to--> Cu + CO2
(4) 4Na + O2 --to--> 2Na2O
(5) Na2O + H2O ---> 2NaOH
(6) S + O2 --to--> SO2
(7) SO2 + H2O ---> H2SO3



\(a.\) Từ \(x-2y=1\) \(\Rightarrow\) \(x=1+2y\) \(\left(\text{*}\right)\)
Thay \(x=1+2y\) vào \(A\), khi đó, biểu thức \(A\) trở thành
\(A=\left(1+2y\right)^2+y^2+4=1+4y+4y^2+y^2+4=5y^2+4y+5\)
\(A=5\left(y^2+\frac{4}{5}y+1\right)=5\left(y^2+2.\frac{2}{5}.y+\frac{4}{25}+\frac{21}{25}\right)=5\left(y+\frac{2}{5}\right)^2+\frac{21}{5}\ge\frac{21}{5}\) với mọi \(y\)
Dấu \(''=''\) xảy ra \(\Leftrightarrow\) \(\left(y+\frac{2}{5}\right)^2=0\) \(\Leftrightarrow\) \(y+\frac{2}{5}=0\) \(\Leftrightarrow\) \(y=-\frac{2}{5}\)
Thay \(y=-\frac{2}{5}\) vào \(\left(\text{*}\right)\), ta được \(x=\frac{1}{5}\)
Vậy, \(A\) đạt giá trị nhỏ nhất là \(A_{min}=\frac{21}{5}\) khi và chỉ khi \(x=\frac{1}{5}\) và \(y=-\frac{2}{5}\)
\(b.\) Gọi \(Q\left(x\right)\) là thương của phép chia và dư là \(r=ax+b\) (vì dư trong phép chia cho \(x^2-1\) có bậc cao nhất là bậc nhất), với mọi \(x\) ta có:
\(x^{2008}-x^3+5=\left(x^2-1\right).Q\left(x\right)+ax+b\) \(\left(\text{**}\right)\)
Với \(x=1\) thì phương trình \(\left(\text{**}\right)\) trở thành \(5=a+b\) \(\left(1\right)\)
Với \(x=-1\) thì phương trình \(\left(\text{**}\right)\) trở thành \(7=-a+b\) \(\left(2\right)\)
Giải hệ phương trình \(\left(1\right)\) và \(\left(2\right)\), ta được \(a=-1\) và \(b=6\)
Vậy, dư trong phép chia đa thức \(x^{2008}-x^3+5\) cho đa thức \(x^2-1\) là \(-x+6\)

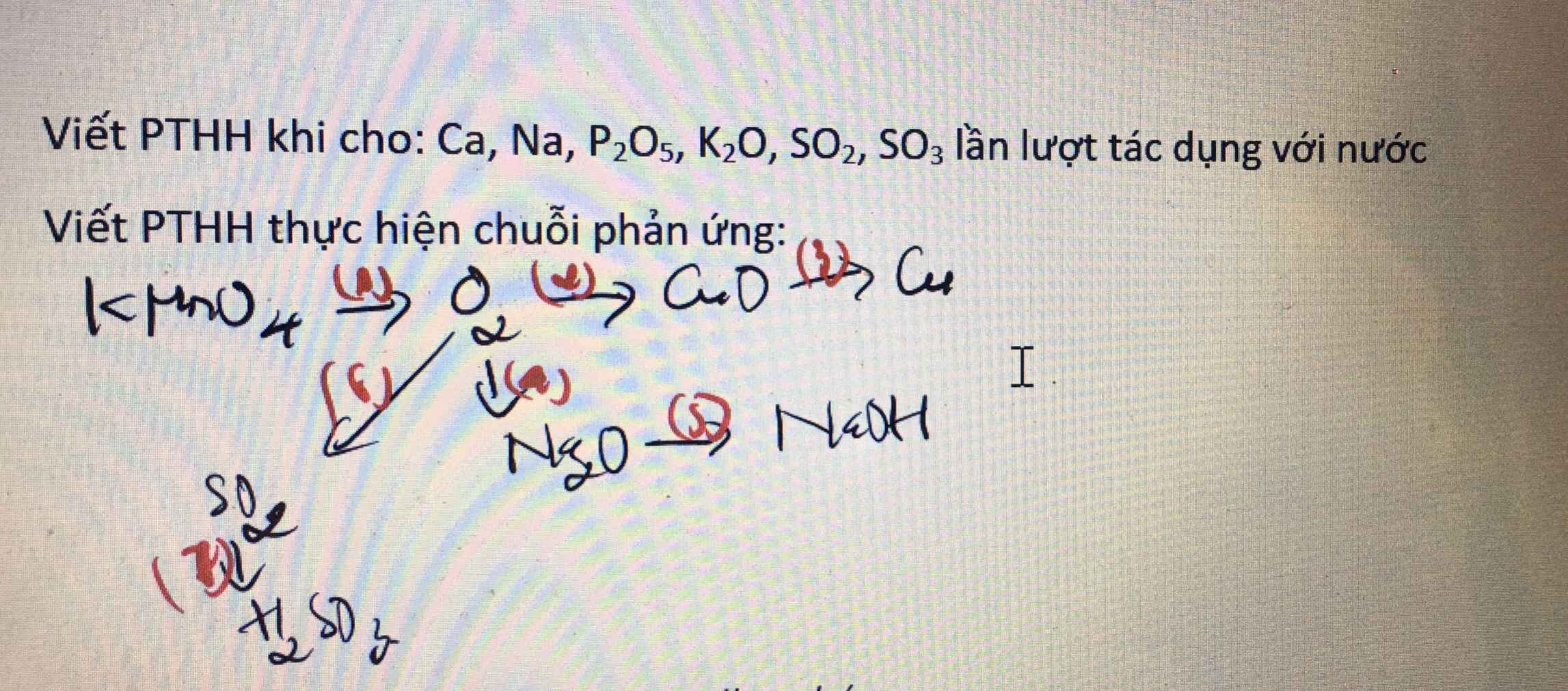

 Hoàn thành
Hoàn thành
B.
b là đúng