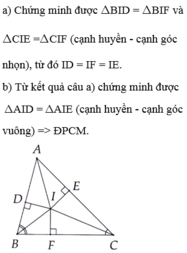
Cho \(\Delta\)ABC, phân giác của góc B và góc C cắt nhau ở I. Vẽ ID\(\perp\)AB tại D, IE\(\perp\)BC tại E, IF\(\perp\)CA tại F. Chứng minh ID=IE=IF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QD
20 tháng 4 2017
Hai tam giác vuông BID và BIE có:
BI là cạnh chung
B1=B2(gt)
nên ∆BID=∆BIE.
(cạnh huyền - góc nhọn)
Suy ra ID=IE (1)
Tương tự ∆CIE=CIF(cạnh huyền góc nhọn).
Suy ra: IE =IF (2)
Từ (1)(2) suy ra: ID=IE=IF.
10 tháng 12 2016
Kí hiệu tam giác viết là t/g nhé
a) BI là phân giác ABC nên ABI = CBI
Xét t/g BID vuông tại D và t/g BIF vuông tại F có:
BI là cạnh chung
DBI = FBI (cmt)
Do đó, t/g BID = t/g BIF ( cạnh góc vuông và góc nhọn kề) (đpcm)
b) t/g BID = t/g BIF (câu a) => ID = IF (2 cạnh tương ứng) (1)
C/m tương tự câu a ta cũng có: t/g ADI = t/g AEI ( cạnh góc vuông và góc nhọn kề)
=> ID = IE (2 cạnh tương ứng)
Từ (1) và (2) => ID = IE = IF (đpcm)
10 tháng 12 2016
ban tu ve hinh nhe
a) Xet tam giac BID va tam giac BIF co:
BI:canh chung
goc DBI=goc IBF(vi tia BI la tia phan giac cua goc DBF)
goc BDI=goc BFI(=90do)
Vay tam giac BID=tam giac BIF(canh huyen, goc nhon)
b) Vi tam giac BID=tam giac BIF(cau a)
Nen ID=IF(2 canh tuong ung) (1)
Xet tam giac AID va tam giac AIE co:
AI:canh chung
goc DAI=goc EAI(vi tia AI la tia phan giac cua goc DAE)
goc ADI=goc AEI(=90do)
Nen tam giac AID=tam giac AIE(canh huyen,goc nhon)
Suy ra:ID=IE(2 canh ung) (2)
Tu (1), (2)\(\Rightarrow\) IF=ID=IE
Chuc ban ngay cang hoc gioi len nhe
Hen gap lai ban vao dip khac nhe
CM
1 tháng 9 2018
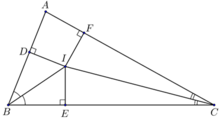
Xét ΔBID (góc D = 90º) và ΔBIE (góc E = 90º) có:
BI là cạnh chung
góc IBD = góc IBE (do BI là tia phân giác góc ABC)
⇒ ΔBID = ΔBIE (cạnh huyền - góc nhọn)
⇒ ID = IE (2 cạnh tương ứng) (1)
Tương tự, xét ΔCIE (góc E = 90º) và ΔCIF (góc F = 90º) có:
CI là cạnh chung
góc ICE = góc ICF (do CI là tia phân giác góc ACB)
⇒ ΔICE = ΔICF (cạnh huyền – góc nhọn)
⇒ IE = IF (2 cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IE = IF (đpcm)
3 tháng 1 2023
Xét ΔBDI vuông tại D và ΔBEI vuông tại E có
BI chung
góc DBI=góc EBI
Do đó: ΔBDI=ΔBEI
=>ID=IE
Xét ΔAEI vuông tại E và ΔAFI vuông tại F có
AI chung
góc EAI=góc FAI
Do đó: ΔAEI=ΔAFI
=>IE=IF=ID
VT
1 tháng 12 2014
Xét 2 TG vuông DBI và EBI, ta có:
DBI=IBE(BI là phân giác của góc B); BI:cạnh chung
=>TG DBI=TG EBI(cạnh huyền- góc nhọn)
=>ID=IE(2 cạnh tương ứng)
Xét 2 TG vuông EIC và FIC, ta có:
ECI=FCI(CI là phân giác góc C); CI:cạnh chung
=>TG EIC=TG FIC(cạnh huyền- góc nhọn)
=>IE=IF(2 cạnh tương ứng)
*Ta có: ID=IE(cmt); IE=IF(cmt)=>ID=IE=IF
4 tháng 12 2018
Xét tam giác BDI và tam giác BEI có
IB(cạnh chung, hay là cạnh huyền)
gócB1=gócB2(gt)
gócD=gócE(=90độ)
suy ra tam giac BDI =tam giác BEI (cạnh huyền, góc nhọn)
suy ra cạnh ID=cạnh IE (2 cạnh tương ứng) (1)
Xét tam giác CEI và tam giác FIC có
IC ( cạnh chung,hay là cạnh huyền)
cạnh IE= cạnh IF(=90độ)
góc C1= góc C2( gt)
suy ra tam giác CEI = tam giác FIC(cạnh huyền, góc nhọn ) (2)
Từ đó ta suy ra ID=IE=IF(đpcm)
Từ (1) và (2) suy ra cạnh
16 tháng 11 2016
Xét tam giác EIC và tam giác FIC có:
IC chung
\(\widehat{ECI}\) = \(\widehat{FCI}\)
\(\widehat{IEC}\) = \(\widehat{IFC}\)
Suy ra 2 tam giác này bằng nhau (1)
xét tam giác DBI và tam giác FBI có:
BI chung
góc FBI bằng góc IBD
góc BDI bằng góc IFB
Suy ra 2 tam giác này bằng nhau (2)
Xét tam giác BIF và tam giác CIF có:
IF chung
góc IFC bằng góc IFB
góc IBF bằng góc ICF
Suy ra hai tam giác này bằng nhau (3)
TỪ (1), (2), (3) TA SUY RA ĐOẠN THẲNG IE = ID = IF ( 3 cạnh tương ứng)