Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cos 6x+cos4x=sin7x-sin3x
=>2*cos5x*cosx=2*cos5x*sin2x
=>cos5x(cosx-sin2x)=0
=>cos5x=0 hoặc sin2x=sin(pi/2-x)
=>5x=pi/2+kpi hoặc 2x=pi/2-x+k2pi hoặc 2x=pi/2+x+k2pi
=>x=pi/10+kpi/5; x=pi/6+k2pi/3; x=pi/2+k2pi

ĐKXĐ: \(x\ne k\pi\)
\(sin7x=sin^2x+2sinx.cos2x+2sinx.cos4x+2sinx.cos6x\)
\(\Leftrightarrow sin7x=sin^2x+sin3x-sinx+sin5x-sin3x+sin7x-sin5x\)
\(\Leftrightarrow sin7x=sin^2x-sinx+sin7x\)
\(\Leftrightarrow sinx\left(sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\left(loại\right)\\sinx=1\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)

\(cosx+cos3x+cos2x+cos4x=0\)
\(\Leftrightarrow2cos2x.cosx+2cos3x.cosx=0\)
\(\Leftrightarrow cosx.\left(cos2x+cos3x\right)=0\)
\(\Leftrightarrow cosx.cos\frac{5x}{2}.cos\frac{x}{2}=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\\cos\frac{5x}{2}=0\\cos\frac{x}{2}=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\\frac{5x}{2}=\frac{\pi}{2}+k\pi\\\frac{x}{2}=\frac{\pi}{2}+k\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{5}+\frac{k2\pi}{5}\\x=\pi+k2\pi\end{matrix}\right.\)
\(sinx+sin7x+sin3x+sin5x=0\)
\(\Leftrightarrow2sin4x.cos3x+2sin4x.cosx=0\)
\(\Leftrightarrow sin4x\left(cos3x+cosx\right)=0\)
\(\Leftrightarrow sin4x.cos2x.cosx=0\)
\(\Leftrightarrow sin4x=0\)
\(\Rightarrow4x=k\pi\Rightarrow x=\frac{k\pi}{4}\)
Lý do chỉ cần 1 pt sin4x=0 do sin4x bao hàm cả cosx và cos2x ở trong đó

\(D=\frac{sin4x+sin5x+sin6x}{cos4x+cos5x+cos6x}\)
\(=\frac{\left(sin4x+sin6x\right)+sin5x}{\left(cos4x+cos6x\right)+cos5x}\)
\(=\frac{2sin\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+sin5x}{2cos\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+cos5x}\)
\(=\frac{2sin5x.cos\left(-x\right)+sin5x}{2cos5x.cos\left(-x\right)+cos5x}=\frac{sin5x\left(2.cos\left(-x\right)+1\right)}{cos5x\left(2.cos\left(-x\right)+1\right)}=\frac{sin5x}{cos5x}=tan5x\)

\(\Leftrightarrow cos6x-cos8x+2\left(1-cos4x\right)^2+\sqrt{3}sin6x=4-4cos4x\)
\(\Leftrightarrow cos6x-cos8x+2\left(1+cos^24x-2cos4x\right)+\sqrt{3}sin6x=4-4cos4x\)
\(\Leftrightarrow cos6x-cos8x+cos8x+3-4cos4x+\sqrt{3}sin6x=4-4cos4x\)
\(\Leftrightarrow cos6x+\sqrt{3}sin6x=1\)
\(\Leftrightarrow cos\left(6x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow...\)

\(\Leftrightarrow2cos4x.cos2x+cos4x=\frac{1}{2}cos2x\left(cos4x+cos2x\right)+2\)
\(\Leftrightarrow3cos4x.cos2x+2cos4x=cos^22x+4\)
\(\Leftrightarrow3cos2x\left(2cos^22x-1\right)+2\left(2cos^22x-1\right)=cos^22x+4\)
\(\Leftrightarrow2cos^22x+cos^22x-cos2x-2=0\)
\(\Leftrightarrow\left(cos2x-1\right)\left(2cos^22x+3cos2x+2\right)=0\)
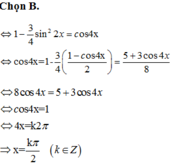
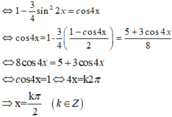

\(\Leftrightarrow2cos5x.cosx=2cos5x.sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=0\\cosx=sin2x=cos\left(\frac{\pi}{2}-2x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{2}-2x+k2\pi\\x=2x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{10}+\frac{k\pi}{5}\\x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)