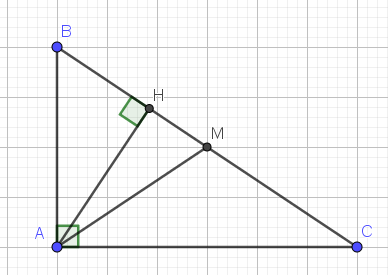
Cho tam giac ABC vuông tại A, đường cao AH.Biết AB, AH=28cm.Kẻ đường phân giác BD của tam giác ABC.Xác định vị trí của điểm M trên cạnh BC để P=Sin AMH + Cos AMH đạt giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
9 tháng 7 2023
Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông:
$144=AH^2=BH.HC(1)$
$BH+CH=BC=25(2)$
Từ $(1); (2)$ áp dụng định lý Viet đảo thì $BH, CH$ là nghiệm của pt: $x^2-25x+144=0$
$\Rightarrow BH, CH= (16,9)$
Mà $AB< AC$ nên $BH< CH$
$\Rightarrow BH=9; CH=16$ (cm)
$AB=\sqrt{BH^2+AH^2}=\sqrt{9^2+12^2}=15$ (cm)
$AC=\sqrt{CH^2+AH^2}=\sqrt{16^2+12^2}=20$ (cm)
b.
$AM=\frac{BC}{2}=\frac{25}{2}$ (cm)
$\sin \widehat{AMH}=\frac{AH}{AM}=\frac{24}{25}$
$\Rightarrow \widehat{AMH}\approx 74^0$
c.
$HM=\sqrt{AM^2-AH^2}=\sqrt{(\frac{25}{2})^2-12^2}=3,5$ (cm)
$S_{AHM}=\frac{AH.HM}{2}=\frac{12.3,5}{2}=21$ (cm2)
12 tháng 7 2023
a: Đặt BH=x; CH=y(x<y)
Theo đề, ta có: xy=12^2=144 và x+y=48
=>x,y là các nghiệm của phương trình:
x^2-48x+144=0
=>x=24-12 căn 3 hoặc x=24+12căn 3
=>BH=24-12căn 3 và CH=24+12căn 3
\(AB=\sqrt{\left(24-12\sqrt{3}\right)\cdot48}\simeq12,42\left(cm\right)\)
\(AC=\sqrt{\left(24+12\sqrt{3}\right)\cdot48}\simeq46,36\left(cm\right)\)
b: AM=BC/2=24cm
sin AMH=AH/AM=12/24=1/2
=>góc AMH=30 độ
16 tháng 3 2023
a: Kẻ BD vuông góc AC,CE vuông góc AB
góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc AED=góc ACB
=>ΔAED đồng dạng vơi ΔACB
Tâm M của đường tròn ngoại tiếp tứ giác BDCE là trung điểm của BC
Gọi H là giao của BD và CE
=>AH vuông góc BC tại N
Gọi giao của OM với (O) là A'
ΔOBC cân tại O
=>OM vuông góc BC
AN<=A'M ko đổi
=>\(S_{ABC}=\dfrac{1}{2}\cdot AN\cdot BC< =\dfrac{1}{2}\cdot A'M\cdot BC_{kođổi}\)
Dấu = xảy ra khi A trùng A'
=>A là điểm chính giữa của cung BC
2 tháng 9 2021
a: Ta có: H và M đối xứng nhau qua AB
nên AB là đường trung trực của MH
Suy ra: AM=AH
Xét ΔAMH có AM=AH
nên ΔAMH cân tại A
mà AB là đường trung trực ứng với cạnh đáy HM
nên AB là tia phân giác của \(\widehat{MAH}\)
S
2 tháng 9 2021
b)
gọi gd của HN và AC là I
gọi gd AB và HM là K
Xét tg HAN có AN là dg trung trực của HN
=> AH=AN=> tg AHN cân tại A.
=> HAI = IAN
Vì AB là pg MAH(cmt)=> MAK =KAH
mà KAH+HAI=A=90 độ
=> MAK+IAN=90 độ
=> MAK+IAN+KAH +HAI=90+90=180 độ
=> A,M,N thẳng hàng (1)
Ta có: tg AMH cân tại A(cmt)=> AM=AH
Tg HAN cân tại A(cmt)=> AH=AN
=> AM=AN. (2)
=> A là td MN
c) xét tg MBH có BK vg góc với MH=> BK là dg cao
MK=KH=> BK là dg ttuyến
=> tg MBH cân tại B(tc tg cân)
=> MB=BH
Chứng minh tương tự cho tg HCN
=> tg HCN cân tại C(tc tg cân)
=> CH=CN
mà BH+HC=BC=> MB+CN=BC