Xét tính chẵn lẻ của hàm số: x5+x4-x3+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
8 tháng 2 2018
Tập xác định D = R\{0} nên nếu x ≠ 0 và x ∈ D thì -x ∈ D
Vậy hàm số đã cho là hàm số lẻ.
PT
1
CM
3 tháng 3 2017
Tập xác định D = R, nhưng f(1) = -1 + 3 - 2 = 0 còn f(-11) = -1 - 3 - 2 = -6 nên f(-1) ≠ f(1) và f(-1) ≠ -f(1)
Vậy hàm số đã cho không là hàm số chẵn cũng không là hàm số lẻ.
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
TXĐ: D=R
\(y\left(-x\right)=\left(-x\right)^3-5\left(-x\right)=-x^3+5x=-\left(x^3-5x\right)=-y\left(x\right)\)
\(\Rightarrow\) Hàm lẻ
CM
5 tháng 5 2017
Đặt y = f(x) = x3 + x.
+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.
+ f(–x) = (–x)3 + (–x) = –x3 – x = – (x3 + x) = –f(x)
Vậy y = x3 + x là một hàm số lẻ.
NT
0
13 tháng 10 2021
TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=\left(-x\right)^4-3\cdot\left(-x\right)^2+1\)
\(=x^4-3x^2+1\)
=f(x)
=> f(x) là hàm số chẵn
24 tháng 7 2018
Xét tích . Giả sử và chẵn, lẻ. Ta có:
Vì chẵn, lẻ nên ở tử và mẫu đều có một số chẵn thừa số, chia đều thành tích các cặp liên tiếp. Theo đề bài thì hai đại lượng liên tiếp tỉ lệ nghịch với nhau nên tích của chúng không đổi.
Các tích trên tử và mẫu đều không đổi Tích không đổi
và tỉ lệ nghịch với nhau.
Vậy đại lượng mang chỉ số chẵn luôn tỉ lệ nghịch với đại lượng mang chỉ số lẻ.
24 tháng 7 2018
Xét tích . Giả sử và chẵn, lẻ. Ta có:
Vì chẵn, lẻ nên ở tử và mẫu đều có một số chẵn thừa số, chia đều thành tích các cặp liên tiếp. Theo đề bài thì hai đại lượng liên tiếp tỉ lệ nghịch với nhau nên tích của chúng không đổi.
Các tích trên tử và mẫu đều không đổi Tích không đổi
và tỉ lệ nghịch với nhau.
Vậy đại lượng mang chỉ số chẵn luôn tỉ lệ nghịch với đại lượng mang chỉ số lẻ.
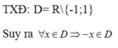
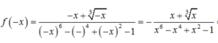
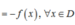
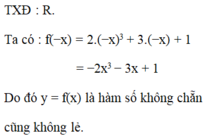
\(f\left(x\right)=x^5+x^4-x^3+1\)
\(f\left(-x\right)=-x^5+x^4+x^3+1\)
Hàm ko chẵn ko lẻ