2. cotang370 . cotang 530 + sin2280 -\(\frac{3.tang54^0}{cotang36^0}\) + sin2 620
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a, Ta có: \({\sin ^2}x + co{s^2}x = 1\)
\(\begin{array}{l} \Leftrightarrow {\sin ^2}\alpha + {\left( {\frac{1}{3}} \right)^2} = 1\\ \Leftrightarrow \sin \alpha = \pm \sqrt {1 - {{\left( {\frac{1}{3}} \right)}^2}} = \pm \frac{{2\sqrt 2 }}{3}\end{array}\)
Vì \( - \frac{\pi }{2} < \alpha < 0\) nên \(sin\alpha < 0 \Rightarrow \sin \alpha = - \frac{{2\sqrt 2 }}{3}\).
\(b)\;\,sin2\alpha = 2sin\alpha .cos\alpha = 2.\left( { - \frac{{2\sqrt 2 }}{3}} \right).\frac{1}{3} = - \frac{{4\sqrt 2 }}{9}\)
\(c)\;cos(\alpha + \frac{\pi }{3}) = cos\alpha .cos\frac{\pi }{3} - sin\alpha .sin\frac{\pi }{3}\)\( = \frac{1}{3}.\frac{1}{2} - \left( { - \frac{{2\sqrt 2 }}{3}} \right).\frac{{\sqrt 3 }}{2} = \frac{{2\sqrt 6 + 1}}{6}\).
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 8 2020
Đề đúng là \(2sin^2\left(5\pi+1\right)\) chứ bạn?
Chứ thấy nó hơi thế nào ấy?
22 tháng 7 2021
a) Ta có: \(A=2\cdot\cot37^0\cdot\cot53^0+\sin^228^0+\sin^262^0-\dfrac{3\cdot\tan54^0}{\cot36^0}\)
\(=2\cdot\tan53^0\cdot\cot53^0+\sin^228^0+\cos^228^0-\dfrac{3\cdot\tan54^0}{\tan54^0}\)
\(=2+1-3\)
=0
QV
Có bao nhiêu giá trị nguyên của m để pt sin2 x - sinx - 3 -m = 0 có nghiệm duy nhất thuộc [-π/2;π/2]
0
NV
2
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
1.
\(\Leftrightarrow2cos2x+sinx-sin3x=0\)
\(\Leftrightarrow2cos2x-2cos2x.sinx=0\)
\(\Leftrightarrow2cos2x\left(1-sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sinx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
2.
\(cos^2x+\left(sin3x-1\right)\left(1-cos\left(\dfrac{\pi}{2}-x\right)\right)=0\)
\(\Leftrightarrow1-sin^2x+\left(sin3x-1\right)\left(1-sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(1+sinx\right)+\left(sin3x-1\right)\left(1-sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(1+sinx+sin3x-1\right)=0\)
\(\Leftrightarrow2\left(1-sinx\right)sin2x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sin2x=0\\cosx=0\end{matrix}\right.\)
\(\Leftrightarrow sin2x=0\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)
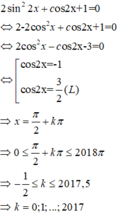
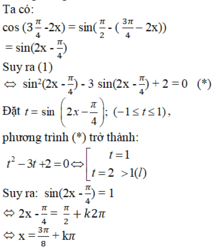
Ta có : \(\cot\left(37\right)=\tan\left(53\right)\) ,\(\sin^2\alpha+\cos^2\alpha=1,\tan\alpha\cdot\cot\alpha=1\)
\(sin\left(28\right)=\cos\left(62\right)\)
\(\Leftrightarrow sin^2\left(28\right)=\cos^2\left(62\right)\)
\(\cot\left(36\right)=\tan\left(54\right)\)
Đề : \(\cot\left(37\right)\cdot\cot\left(53\right)+\sin^2\left(28\right)-\frac{3\cdot\tan\left(54\right)}{\cot\left(36\right)}+sin^2\left(62\right)\)
\(=\tan\left(53\right)\cdot\cot\left(53\right)+\cos^2\left(62\right)-\frac{3\cdot\tan\left(54\right)}{\tan\left(54\right)}+\sin^2\left(62\right)\)
\(=\)\(\tan\left(53\right)\cdot\cot\left(53\right)+\cos^2\left(62\right)+\sin^2\left(62\right)-\frac{3\cdot\tan\left(54\right)}{\tan\left(54\right)}\)
\(=1+1-3\)
\(=-1\)