gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đồ thị hàm số y= x2-10x-2m+5 cắt trục hoành tại 2 điểm phân biệt có hoành độ dương . tính số phần tử của S
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Phương trình hoành độ giao điểm của (C) và đường thẳng d:
=x4- (2m-1) x2+2m = 2 hay x4- (2m-1) x2+2m -2=0
Suy ra x2= 1 hoặc x2= 2m-2 (1)
+ Đường thẳng d cắt C tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương trình (1) có hai nghiệm phân biệt nhỏ hơn 3.
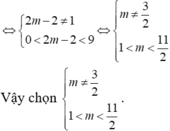
Do đó có 4 giá trị nguyên của m thỏa mãn đầu bài.
Chọn D.

Đáp án C
Phương trình hoành độ giao điểm là: m x 3 - x 2 2 x + 8 m = 0
⇔ m x + 2 x 2 - 2 x + 4 - x x + 2 = 0 ⇔ x + 2 m x 2 - 2 m x + 4 m - x = 0 ⇔ [ x = - 2 g x = m x 2 - 1 + 2 m x + 4 m = 0
Để đồ thị C m cắt trục hoành tại ba điểm phân biệt thì g x = 0 có 2 nghiệm phân biệt khác -2 ⇔ m ≠ 0 ∆ = 1 + 2 m 2 - 16 m 2 > 0 g - 2 = 4 m + 2 1 + 2 m + 4 m ≠ 0 ⇔ m ∈ - 1 6 ; 1 2 \ 0


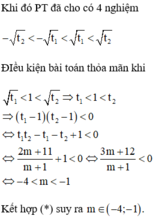




Phương trình hoành độ giao điểm:
\(x^2-10x-2m+5=0\)
\(\Delta'=25+2m-5>0\Rightarrow m>-10\)
Theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=10\\x_1x_2=-2m+5\end{matrix}\right.\)
Để pt đã cho có 2 nghiệm dương \(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\)
\(\Rightarrow-2m+5>0\Rightarrow m< \frac{5}{2}\)
\(\Rightarrow m=\left\{-9;-8;...;1;2\right\}\)
\(\Rightarrow\sum m=-42\)