Vật có khối lượng m= 20kg được kéo chuyển động ngang bởi lực F hợp với phương ngang góc \(\alpha\)độ lớn F =120N. hệ số ma sát \(\mu\) Nếu \(\alpha=\alpha_1\) =60 độ thì vật chuyển động đều . Tìm gia tốc của chuyển động nếu \(\alpha=\alpha_2\) =30 độ lấy g=10m/s2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Vật chuyển động thẳng đều:
Lực ma sát:
\(F_{ms}=\mu mg=0,1\cdot5\cdot10=5N\)
\(\Rightarrow F_k=P=10m=10\cdot5=50N\)
b)Sau khi chuyển động đc 2s:
Vật chuyển động trên mặt phẳng nằm ngang thì theo định luật ll Niu-tơn ta có:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
Gia tốc vật: \(S=\dfrac{1}{2}at^2\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2\cdot5}{2^2}=2,5\)m/s2
Chọn chiều dương là chiều chuyển động.
\(\Rightarrow F-F_{ms}=m\cdot a\)
\(\Rightarrow F=m\cdot a+F_{ms}=5\cdot2,5+5=17,5N\)

Áp dụng ĐL II Newton có:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m\overrightarrow{a}\) (*)
a. Để vật chuyển động thẳng đều thì \(a=0\)
Chiếu (*) lên phương thẳng đứng có:
\(N=P=mg=60\) (N)
Chiếu (*) lên phương chuyển động có:
\(F\cos45^o=F_{ms}\)
\(\Rightarrow F=\dfrac{0,1.60}{\cos45^o}=8,5\) (N)
b. Gia tốc của vật là:
\(a=\dfrac{2s}{t^2}=\dfrac{2.8}{4^2}=1\) (m/s2)
Khi đó:
\(F\cos45^o-F_{ms}=ma\)
\(\Rightarrow F=\dfrac{6.1+0,1.60}{cos45^o}=16,97\) (N)

Tham khảo:
`*` Gia tốc của vật:
\(S=\dfrac{a.t^2}{2}\)
\(\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2.1,66}{2^2}=0,83(m/s^2)\)
`*` Theo đinh luật II Newton chiếu lên chiều dương:
\(F.cosα-F_{ms}=m.a\)
\(\Rightarrow F_{ms}=F.cosα - m.a=2.cos30- 0,83=0,9(N) \)
`*` Hệ số ma sát:
\(F_{ms}=0,9=μ.m.g=2N=>μ=0,2\)
Tham khảo:
⋅⋅ Gia tốc của vật:
S=a.t22S=a.t22
⇒a=2St2=2.1,6622=0,83(m/s2)⇒a=2St2=2.1,6622=0,83(m/s2)
⋅⋅ Theo đinh luật II Newton chiếu lên chiều dương:
F.cosα−Fms=m.aF.cosα−Fms=m.a
⇒Fms=F.cosα−m.a=2.cos30−0,83=0,9(N)⇒Fms=F.cosα−m.a=2.cos30−0,83=0,9(N)
⋅⋅ Hệ số ma sát:
Fms=0,9=μ.m.g=2N=>μ=0,2
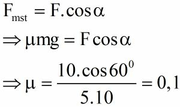
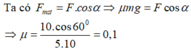
Vì vật chuyển động đều
\(\Rightarrow\overrightarrow{F}+\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F_{ms}}=\overrightarrow{0}\)
Chọn trục toạ độ có trục hoành hướng sang phải, trục tung hướng lên
\(\Rightarrow\left\{{}\begin{matrix}Ox:F.\cos\alpha-F_{ms}=0\\Oy:F.\sin\alpha+N-P=0\end{matrix}\right.\)
\(\Rightarrow F.\cos\alpha-\mu.\left(P-F.\sin\alpha\right)=0\)
\(\Leftrightarrow120.\cos60-\mu.\left(200-120.\sin60\right)=0\)
=> \(\mu=...\)
Tìm gia tốc trong trường hợp alpha= 300 thì lúc này vật chuyển động biến đổi đều nên có gia tốc, tức là \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Cậu chiếu lên trục toạ độ rồi phân tích, bt hệ số ma sát rồi thì tìm a ez