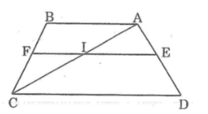
Trên các cạnh AB và CD của hình chữ nhật ABCD ( AD < AB ) , ta lấy các điểm F và E sao cho AFCE là hình thoi . Tính EF , biết rằng AB = 16 và BC = 12 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
F
28 tháng 10 2017
a.Xét ΔAME và ΔCNF có
AM=CN(gt)
Góc MAE= góc NCF
AE=CF(gt)
Do đó ΔAME = ΔCNF (c.g.c)
=> ME=NF(2 cạnh tương ứng)
Tương tự ΔDMF= ΔBNE(c.g.c)
=>MF=NE(2 cạnh tương ứng)
Tứ giác EMFN có
ME=NF(gt)
MF=NE(gt)
=>EMFN là hình bình hành
b) b/ Ta có: OE=OF (MENF là hình bình hành)
ON=OM(MENF là hình bình hành)
OD=OB (ABCD là hình bình hành)
OA=OC(ABCDlà hình bình hành)
=>AC, BD, MN, E giao nhau tại O
hay AC, BD, MN, EF đồng quy
cn lại bó tay
CM
22 tháng 12 2019
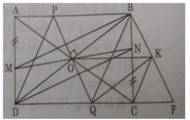
c) PQ ⊥ BD (gt). Xét các tam giác vuông POB và QOD có:
∠POB = ∠QOD∠ (đối đỉnh),
OB = OD
∠PBO = ∠QDO (so le trong).
Do đó ΔPOB = ΔQOD (g.c.g) ⇒ BP = DQ
Lại có BP // DQ nên tứ giác PBQD là hình bình hành
Mặt khác PBQD có hai đường chéo vuông góc nên là hình thoi.
12 tháng 5 2023
Chiều rộng là: 24:2-8=4(cm)
EG=AD=4cm
HF=AB=8cm
\(S_{EFGH}=\dfrac{1}{2}\cdot4\cdot8=16\left(cm^2\right)\)
CM
14 tháng 10 2019
Kẻ đường chéo AC cắt EF tại I
Trong ΔADC, ta có: EI // CD
Suy ra: 
Suy ra: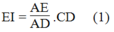 
Lại có :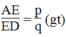 
Suy ra: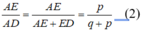 
Từ (1) và (2) suy ra: 
Trong ΔABC, ta có: FI // AB
Suy ra: 
(định lí ta-lét) (3)
Trong ΔADC, ta có : EI // CD
Suy ra: 
(định lí ta-lét) (4)
Từ (3) và (4) suy ra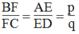 
Trong ΔABC, ta có: IF // AB
Suy ra: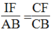 
(định lí ta-lét)
Suy ra: 
Ta có: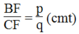 
Suy ra: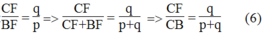 
Từ (5) và (6) suy ra: 
Vậy: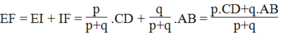 
CH
Cô Hoàng Huyền
Admin
VIP
6 tháng 10 2017
a) Do F đối xứng với C qua BE nên EB là đường trung trực của FC.
Vậy thì ta có ngay \(\Delta BFE=\Delta BCE\left(c-c-c\right)\Rightarrow\widehat{BFE}=\widehat{BCE}=90^o\)
Vậy thì \(\widehat{AFB}+\widehat{DFE}=90^o\)
Lại có góc DFE và góc AFQ là hai góc đối đỉnh nên \(\widehat{AFB}+\widehat{AFQ}=90^o\Rightarrow\widehat{AFB}=\widehat{AQF}\)
Vậy \(\Delta AQF\sim\Delta AFB\left(g-g\right)\)
b) Từ E kẻ \(EJ\perp QB\). Khi đó ta có EJ = BC. Gọi I là giao điểm của QC và BD.
Do AF// JE nên \(\Delta AQF\sim\Delta JQE\). Vậy thì \(\Delta JQE\sim\Delta DEF\left(\sim\Delta AQF\right)\)
\(\Rightarrow\frac{JE}{DF}=\frac{QE}{EF}\)
Hay \(\frac{BC}{DF}=\frac{QE}{EF}\Rightarrow\frac{BF}{DF}=\frac{QE}{EC}\left(1\right)\) (Do BE là trung trực nên BC = BF, FE = EC)
Ta cũng đã có \(\widehat{FED}=\widehat{AFB}\Rightarrow\widehat{QEC}=\widehat{BFD}\left(2\right)\)
Từ (1) và (2) suy ra \(\Delta QEC\sim\Delta BFD\left(c-g-c\right)\)
\(\Rightarrow\widehat{FQC}=\widehat{FBD}\)
Lại có \(\widehat{BFQ}=\widehat{BFA}+\widehat{AFQ}=90^o\)
Vậy nên \(\widehat{FQB}+\widehat{QBF}=\widehat{FQC}+\widehat{CQB}+\widehat{QBF}=\widehat{CQB}+\widehat{QBD}=90^o\)
Suy ra \(\widehat{AIB}=90^o\Rightarrow QC\perp BD.\)