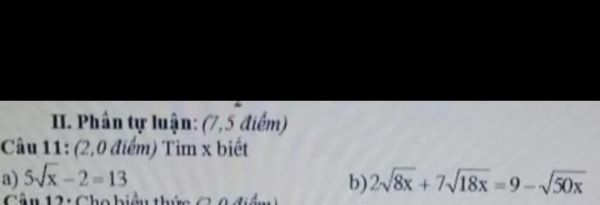
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta thấy \(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\) và \(x^2+y^2=\left(x+y\right)^2-2xy\) nên nếu đặt \(x+y=S,xy=P\) thì ta có hệ: \(\left\{{}\begin{matrix}S^3-3SP=2\\S^2-2P=2\end{matrix}\right.\) . Từ pt (2) suy ra \(P=\dfrac{S^2-2}{2}\). Thay vào (1), ta có \(S^3-3S.\dfrac{S^2-2}{2}=2\) \(\Leftrightarrow-S^3+6S-4=0\) hay \(S^3-6S+4=0\)
Đến đây ta dễ dàng nhẩm ra được \(S=2\). Do đó ta lập sơ đồ Horner:
| \(x\) | 1 | 0 | -6 | 4 |
| \(2\) | 1 | 2 | -2 | 0 |
Nghĩa là từ \(S^3-6S+4=0\) ta sẽ có \(\left(S-2\right)\left(S^2+2S-2\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}S=2\\S=-1\pm\sqrt{3}\end{matrix}\right.\).
Nếu \(S=2\) thì \(P=\dfrac{S^2-2}{2}=1\). Ta thấy \(S^2-4P=0\) nên x, y sẽ là nghiệm của pt \(X^2-2X+1=0\Leftrightarrow\left(X-1\right)^2=0\Leftrightarrow X=1\) hay \(\left(x;y\right)=\left(1;1\right)\).
Nếu \(S=-1+\sqrt{3}\) thì \(P=\dfrac{S^2-2}{2}=1-\sqrt{3}\). Ta thấy \(S^2-4P>0\) nên x, y là nghiệm của pt \(X^2-\left(\sqrt{3}-1\right)X+1-\sqrt{3}=0\). \(\Delta=2\sqrt{3}\) nên \(X=\dfrac{\sqrt{3}-1\pm\sqrt{2\sqrt{3}}}{2}\) hay \(\left(x;y\right)=\left(\dfrac{\sqrt{3}-1+\sqrt{2\sqrt{3}}}{2};\dfrac{\sqrt{3}-1-2\sqrt{3}}{2}\right)\) và hoán vị của nó.
Nếu \(S=-1-\sqrt{3}\) thì \(P=\dfrac{S^2-2}{2}=1+\sqrt{3}\). Mà \(S^2-4P=-2\sqrt{3}< 0\) nên không tìm được nghiệm (x; y)
Như vậy hệ phương trình đã cho có các cặp nghiệm \(\left(1;1\right);\left(\dfrac{\sqrt{3}-1+\sqrt{2\sqrt{3}}}{2};\dfrac{\sqrt{3}-1-\sqrt{2\sqrt{3}}}{2}\right)\)\(\left(\dfrac{\sqrt{3}-1-\sqrt{2\sqrt{3}}}{2};\dfrac{\sqrt{3}-1+2\sqrt{3}}{2}\right)\)
b) Ta thấy \(x^3+y^3+xy=\left(x+y\right)^3-3xy\left(x+y\right)+xy\) nên nếu đặt \(S=x+y,P=xy\) thì ta có hệ \(\left\{{}\begin{matrix}S^3-3SP+P=3\\S+P=3\end{matrix}\right.\), suy ra \(P=3-S\)
\(\Rightarrow S^3-3S\left(3-S\right)+3-S=3\)
\(\Leftrightarrow S^3-10S+3S^2=0\)
\(\Leftrightarrow S\left(S^2+3S-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}S=0\\S=2\\S=-5\end{matrix}\right.\)
Nếu \(S=0\) thì \(P=3\). Khi đó vì \(S^2-4P< 0\) nên không tìm được nghiệm (x; y)
Nếu \(S=2\) thì suy ra \(P=1\). Ta có \(S^2-4P=0\) nên x, y là nghiệm của pt \(X^2-2X+1=0\Leftrightarrow X=1\) hay \(\left(x;y\right)=\left(1;1\right)\)
Nếu \(S=-5\) thì suy ra \(P=8\). Ta có \(S^2-4P< 0\) nên không thể tìm được nghiệm (x; y).
Như vậy hpt đã cho có nghiệm duy nhất \(\left(1;1\right)\)

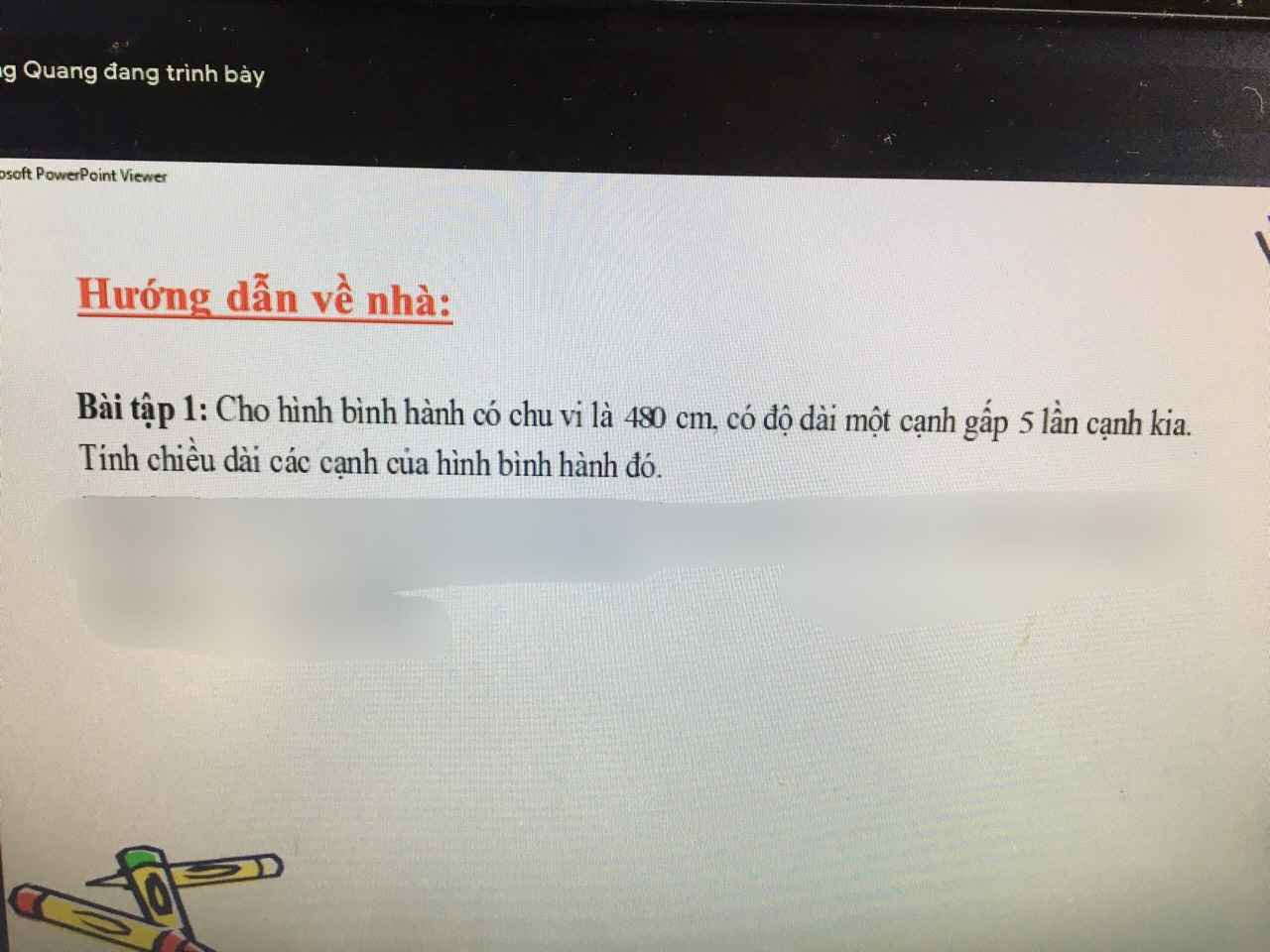
Chiều dài cạnh lớn là:
240:6x5=200(cm)
Chiều dài cạnh nhỏ là:
240-200=40(cm)
Chiều dài cạnh lớn là:
240:6x5=200(cm)
Chiều dài cạnh nhỏ là:
240-200=40(cm)

a, \(\sqrt{x^2-6x+9}=2\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}=2\)
\(\Leftrightarrow\left|x-3\right|=2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=2\\x-3=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)
a: Ta có: \(\sqrt{x^2-6x+9}=2\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)


a: \(M=2\left(x+5\right)^2+5\left(x-2\right)^2-7\left(x+3\right)\left(x-3\right)\)
\(=2\left(x^2+10x+25\right)+5\left(x^2-4x+4\right)-7\left(x^2-9\right)\)
\(=2x^2+20x+50+5x^2-20x+20-7x^2+63\)
\(=113\)
b: \(H=\left(2x-3y\right)^2-\left(3y-2\right)\left(3y+2\right)-\left(1-2x\right)^2+4x\left(3y-1\right)\)
\(=4x^2-12xy+9y^2+12xy-4x-\left(9y^2-4\right)-\left(4x^2-4x+1\right)\)
\(=4x^2+9y^2-4x-9y^2+4-4x^2+4x-1\)
=3
c: \(N=\left(2x+3y\right)^2+\left(3x-2y\right)^2-13\left(x+y\right)\left(x-y\right)-26\left(y+1\right)\left(y-1\right)\)
\(=4x^2+12xy+9y^2+9x^2-12xy+4y^2-13\left(x^2-y^2\right)-26\left(y^2-1\right)\)
\(=13x^2+13y^2-13x^2+13y^2-26y^2+26\)
=26
d: \(K=\left(x^2y-3\right)^2-\left(2x-y\right)^3+xy^2\left(6-x^3\right)+8x^3-6x^2y-y^3\)
\(=x^4y^2-6x^2y+9+6xy^2-x^4y^2+8x^3-6x^2y-y^3-\left(2x-y\right)^3\)
\(=-12x^2y+9-y^3+6xy^2+8x^3-\left(8x^3-12x^2y+6xy^2-y^3\right)\)
\(=\left(8x^3-12x^2y+6xy^2-y^3\right)-\left(8x^3-12x^2y+6xy^2-y^3\right)+9\)
=9
e: \(P=\left(4x+3\right)\left(16x^2-12x+9\right)-\left(-23+64x^3\right)\)
\(=\left(4x\right)^3+3^3+23-64x^3\)
\(=64x^3+27+23-64x^3\)
=50
h: \(Q=\left(x+5y\right)\left(x^2-5xy+25y^2\right)+\left(x-5y\right)\left(x^2+5xy+25y^2\right)-\dfrac{1}{2}\left(4x^3-7\right)\)
\(=x^3+125y^3+x^3-125y^3-2x^3+\dfrac{7}{2}\)
=7/2

IV.
21. a -> an
22. polluted -> pollution
23. noisy -> noisier
24. Lucky -> Luckily
25. learning -> to learn
V.
26. visit her friend because she doesn't have time.
27. how much I thought it would cost.
28. gone aboard before.
29. been used for three months.
30. is considered to be one of the best.
IV:
21. an hour
22.
23. noisier
24. Luckily
25. to learn
V:
26.
She won't visit her friends because she hasn't time.
27.
He asked me how much I thought it would cost.
28
He hasn't gone abroad before.
29.
That computer has been used for 3 months.
30.
His speech was considered one of the best

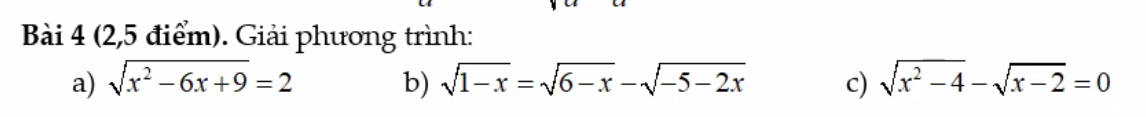



Trả lời:
a, \(5\sqrt{x}-2=13\left(ĐK:x\ge0\right)\)
\(\Leftrightarrow5\sqrt{x}=15\)
\(\Leftrightarrow\sqrt{x}=3\)
\(\Leftrightarrow x=9\left(tm\right)\)
Vậy x = 9
b, \(2\sqrt{8x}+7\sqrt{18x}=9-\sqrt{50x}\left(ĐK:x\ge0\right)\)
\(\Leftrightarrow2\sqrt{2^2.2x}+7\sqrt{3^2.2x}=9-\sqrt{5^2.2x}\)
\(\Leftrightarrow4\sqrt{2x}+21\sqrt{2x}=9-5\sqrt{2x}\)
\(\Leftrightarrow4\sqrt{2x}+21\sqrt{2x}+5\sqrt{2x}=9\)
\(\Leftrightarrow30\sqrt{2x}=9\)
\(\Leftrightarrow\sqrt{2x}=\frac{3}{10}\)
\(\Leftrightarrow2x=\frac{9}{100}\)
\(\Leftrightarrow x=\frac{9}{200}\left(tm\right)\)
Vậy x = 9/200