Cho góc nhìn xOy , kể thêm tia phân giác Oz. Trên tia Ox lấy A, Oy lấy B sao cho OA=OB. Trên Oz lấy điểm I bất kì. Chứng minh OI là đường trung trực của AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2021
a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
12 tháng 9 2021
a: Xét ΔAOI và ΔBOI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔAOI=ΔBOI
Suy ra: IA=IB
18 tháng 8 2023
Ta có hình vẽ:
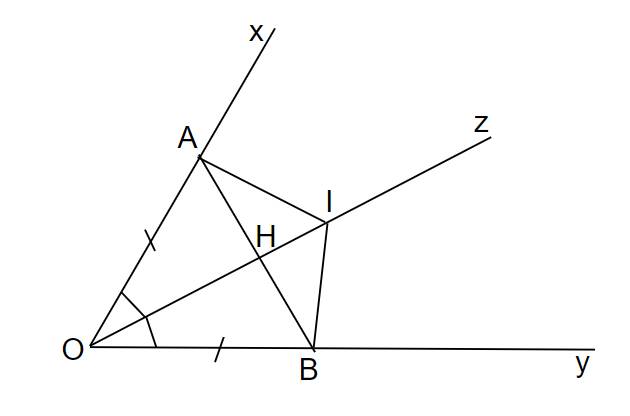
a) Vì Oz là phân giác của xOy nên
Xét Δ AOI và Δ BOI có:
OA = OB (gt)
AOI = BOI (cmt)
OI là cạnh chung
Do đó, Δ AOI = Δ BOI (c.g.c) (đpcm)
b) Xét Δ AOH và Δ BOH có:
OA = OB (gt)
AOH = BOH (câu a)
OH là cạnh chung
Do đó, Δ AOH = Δ BOH (c.g.c)
=> AHO = BHO (2 góc tương ứng)
Mà AHO + BHO = 180o (kề bù) nên AHO = BHO = 90o
=>
28 tháng 6 2017
Xét \(\Delta\)AOM và \(\Delta\)BOM có:
OA=OB (gt)
góc AOM=góc BOM (do Oz là phân giác góc xOy)
OM chung
=> \(\Delta\)AOM = \(\Delta\)BOM (c.g.c) (1)
(1) => góc AMO=góc BMO (2 góc tương ứng)
=> MO là phân giác góc AMB (dpcm)
(1) => AM=BM (2 góc tương ứng)
=> \(\Delta\)ABM cân tại M (dhnb)
Xét \(\Delta\)ABM cân tại M có tia phân giác MO đồng thời là đường trung trực của cạnh AB (t/c các đường đặc biệt trong \(\Delta\)cân) (dpcm)