Cho tam giác nhọn ABC nội tiếp đường tròn (O). M là điểm bất kì thuộc cung BC không chứa A. Gọi D, E theo thứ tự là các điểm đối xứng với M qua AB, AC. Tìm vị trí của M để DE có độ dài lớn nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 8 2021
Do D đối xứng M qua AB \(\Rightarrow\) AB là trung trực DM
\(\Rightarrow AM=AD\) và \(\widehat{DAB}=\widehat{MAB}\)
Tương tự ta có \(AM=AE\) và \(\widehat{CAM}=\widehat{CAE}\)
\(\Rightarrow\widehat{DAE}=\widehat{DAB}+\widehat{MAB}+\widehat{CAM}+\widehat{CAE}=2\left(\widehat{MAB}+\widehat{CAM}\right)=2\widehat{BAC}\)
Do \(AM=AD=AE\Rightarrow\Delta ADE\) cân tại A
Kẻ đường cao AH ứng với DE \(\Rightarrow\) H đồng thời là trung điểm DE và \(\widehat{DAH}=\dfrac{1}{2}\widehat{DAE}=\dfrac{1}{2}.2\widehat{BAC}=\widehat{BAC}\)
Trong tam giác vuông ADH:
\(sin\widehat{DAH}=\dfrac{DH}{AD}\Rightarrow DH=AD.sin\widehat{DAH}=AM.sin\widehat{BAC}\)
\(\Rightarrow\dfrac{1}{2}DE=AM.sin\widehat{BAC}\Rightarrow DE=2AM.sin\widehat{BAC}\)
Mà ABC cố định \(\Rightarrow DE_{max}\) khi \(AM_{max}\Rightarrow AM\) là đường kính của đường tròn
Hay M đối xứng A qua tâm O
CM
28 tháng 5 2019
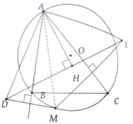
Kẻ AH ⊥ DE tại H
D A E ^ = 2 B A C ^
=> D A H ^ = B A C ^
Từ DE=2DH; AD=AM=AE
Suy ra DH=AD.sin D A H ^
Từ đó D E m a x <=> AM = 2R
VT
24 tháng 2 2021
1. Gọi giao điểm của CH với AB là I, AH với BC là K,Ta có tứ giác BIHK nội tiếp mà (1) Ta lại có (hai góc nội tiếp cùng chắn một cung)
(t/c đối xứng) (2)Từ (1) và (2) Suy ra tứ giác AHCP nội tiếp.2. Tứ giác AHCP nội tiếp Ta lại có mà
(3)Chứng minh tương tự câu 1) ta có tứ giác AHBN nội tiếp
(4)
Từ (3) và (4) N, H, P thẳng hàng
3.
=> (<180độ) không đổi
Có AN = AM = AP, cần chứng minh NP = 2.AP.sinBAC
=> NP lớn nhất <=> AP lớn nhất mà AP = AM
AM lớn nhất <=> AM là đường kính của đường tròn (O)
Vậy NP lớn nhất <=> AM là đường kính của đường tròn.
24 tháng 2 2021
a)gọi I là giao điểm của CH và AB
K là giao điểm AH và BC
ta có :góc IBK+ AHC=180 độ
mà góc IBK= APC
=> tứ giác AHCP nội tiếp
b)Ta có Góc AHP= ACP cùng chắn cung AP (
mà góc ACP=ACM (1)
=> góc ACP= AHP
cmtt
gócAHN=ABN cùng chắn cung AP
mà ABN=ABM => AHN=ABM(2)
Xét tứ giác ABMC nội tiếp
gócACM+ABM=180 độ (3)
từ (1)(2)(3) =>
góc AHP+AHN=180 độ
=> N,H,P thẳng hàng
ta có góc MAN=2BAM,
góc MAP=2MAC
=> NAP=2(BAM+MAC)
=2 x góc BAC (ko đổi )
ta có AM=AN=AP
NP=2AP.sin BAC=2AM.sinBAC
=> NP lớn nhất <=> AM Max
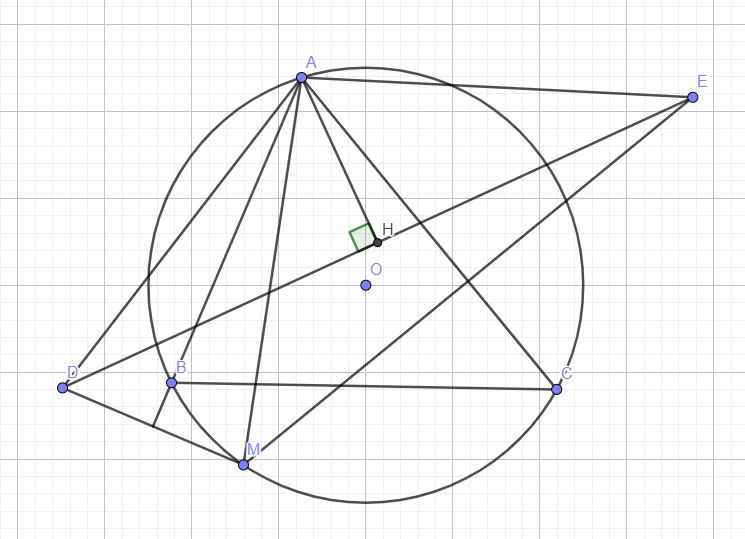
Tham khảo: