Ở hình 32 , biết a // b , \(\widehat{A}\) = 90'( độ ) , \(\widehat{C}\) = 130'( độ ) , tính \(\widehat{B}\) , \(\widehat{D}\)
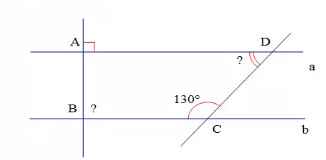 Hình 32
Hình 32
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có a // b, nên
góc B = góc A = 90 độ (đồng vị)
Ta lại có \(\widehat{C}+\widehat{D}=180^o\)
hay \(130^o+\widehat{D}=180^o\Rightarrow\widehat{D}=180^o-130^o=50^o\)
vậy góc B = 90 độ
góc C = 50 độ

a) Các góc kề với \(\widehat {xOy}\) là: \(\widehat {yOz};\widehat {yOt}\)
b) Ta có:
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} + \widehat {zOt} = \widehat {xOt}\\ \Rightarrow 20^\circ + \widehat {zOt} + \widehat {zOt} = 90^\circ \\ \Rightarrow 2.\widehat {zOt} = 90^\circ - 20^\circ = 70^\circ \\ \Rightarrow \widehat {zOt} = 70^\circ :2 = 35^\circ \end{array}\)

a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)

Vì Ax // Dy, mà AD \( \bot \) Ax nên AD \( \bot \) Dy. Do đó, \(\widehat{ADC}=90^0\)
Vì Ax // Dy nên \(\widehat {ABC} = \widehat {BCy}\) ( 2 góc so le trong), mà \(\widehat {BCy} = 50^\circ \Rightarrow \widehat {ABC} = 50^\circ \)
Vậy \(\widehat{ADC}=90^0; \widehat {ABC} = 50^\circ \)

Hình tự vẽ nhé
a,
Gọi H là chân đường cao hạ từ C, ABCH là hình vuông
\(\Rightarrow CH=BC=\frac{AD}{2}\)
Tam giác CDH có:
\(\widehat{CHD=90^o;CH=HD}\)
\(\Rightarrow CHD\)là tam giác vuông cân tại H
\(\Rightarrow\widehat{CDH}=\widehat{HCD}=45^o\)
\(\Rightarrow\widehat{BCD}=90^o+45^o=135^o\)
b, Có CH = AH
\(\Rightarrow\)Tam giác AHC vuông cân tại H. Do đó \(\widehat{ACH}=45^o\)
Mà \(\widehat{HCD}=45^o\)
\(\Rightarrow\widehat{ACD}=45^o+45^o=90^o\)
Vậy \(AC\perp CD\)( đpcm )
\(a//b;a\perp AB\Rightarrow b\perp AB\Rightarrow\widehat{B}=90^0\)
\(a//b\Rightarrow\widehat{D}+\widehat{C}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{D}=180^0-130^0=50^0\)
a,Ta thấy \(\widehat{B}\) là góc vuông
\(\Rightarrow\widehat{B}=90^o\)
\(\widehat{C}+\widehat{D}=180^o\)(bù nhau)
\(\Rightarrow\widehat{D}=180^o-130^o=50^o\)