Cho \(\overrightarrow{u}=2\overrightarrow{i}-\overrightarrow{j}\), \(\overrightarrow{v}=\overrightarrow{i}+x\overrightarrow{j}\). Tìm x để \(\overrightarrow{u}\) và \(\overrightarrow{v}\) cùng phương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 12 2022
\(\overrightarrow{u}=\left(\dfrac{1}{2};-5\right);\overrightarrow{v}=\left(k;-4\right)\)
để vecto u vuông góc với vecto v thì 1/2*k+(-4)*(-5)=0
=>k*1/2=-20
=>k=-40
TS
14 tháng 10 2018
Ta có: \(\overrightarrow{u}=\left(\dfrac{1}{2};-5\right)\) ; \(\overrightarrow{v}=\left(k;-4\right)\)
Để hai vectơ \(\overrightarrow{u}\) và \(\overrightarrow{v}\) cùng phương
\(\Leftrightarrow\dfrac{k}{\dfrac{1}{2}}=\dfrac{4}{5}\Leftrightarrow k=\dfrac{2}{5}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) Ta có hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \) vuông góc nên \(\overrightarrow i .\overrightarrow j = 0\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} + 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \({\left( {\overrightarrow i + \overrightarrow j } \right)^2} = {\left( {\overrightarrow i } \right)^2} + {\left( {\overrightarrow j } \right)^2} - 2\overrightarrow i .\overrightarrow j = {\left| {\overrightarrow i } \right|^2} + {\left| {\overrightarrow j } \right|^2} = 1 + 1 = 2\)
+) \(\left( {\overrightarrow i + \overrightarrow j } \right)\left( {\overrightarrow i - \overrightarrow j } \right) = {\left( {\overrightarrow i } \right)^2} - {\left( {\overrightarrow j } \right)^2} = {\left| {\overrightarrow i } \right|^2} - {\left| {\overrightarrow j } \right|^2} = 1 - 1 = 0\)
b) Sử dụng kết quả của câu a) ta có:
\(\overrightarrow a .\overrightarrow b = \left( {2\overrightarrow i + 2\overrightarrow j } \right).\left( {3\overrightarrow i - 3\overrightarrow j } \right) = 2.3.\left( {\overrightarrow i + \overrightarrow j } \right).\left( {\overrightarrow i - \overrightarrow j } \right) = 6.0 = 0\)
\(\overrightarrow a .\overrightarrow b = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ \)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Tọa độ của vectơ \(\overrightarrow a \) là \(\left( {2;7} \right)\)
b) Tọa độ của vectơ \(\overrightarrow b \) là \(\left( { - 1;3} \right)\)
c) Tọa độ của vectơ \(\overrightarrow c \) là \(\left( {4;0} \right)\)
d) Tọa độ của vectơ \(\overrightarrow d \) là \(\left( {0; - 9} \right)\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Vì \(\overrightarrow a = 3\overrightarrow i \)nên \(\overrightarrow a = \left( {3;0} \right)\)
b) Vì \(\overrightarrow b = - \overrightarrow j \)nên \(\overrightarrow b = \left( {0; - 1} \right)\)
c) Vì \(\overrightarrow c = \overrightarrow i - 4\overrightarrow j \)nên \(\overrightarrow c = \left( {1; - 4} \right)\)
d) Vì \(\overrightarrow d = 0,5\overrightarrow i + \sqrt 6 \overrightarrow j \)nên \(\overrightarrow d = \left( {0,5;\sqrt 6 } \right)\)
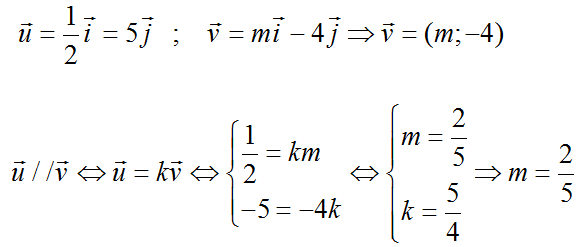
Có \(\overrightarrow{u}=\left(2;-1\right);\overrightarrow{v}=\left(1;x\right)\)
\(\overrightarrow{u}\) cùng phg vs \(\overrightarrow{v}\)
\(\Leftrightarrow\frac{1}{2}=\frac{-x}{1}\Leftrightarrow x=-\frac{1}{2}\)