Một xe chuyển động thẳng không đổi chiều; 2 giờ đầu xe chạy với vận tốc trung bình 60 km/h, 3 giờ sau xe chạy với vận tốc trung bình 40 km/ h. Tính vận tốc trung bình của xe trong suốt thời giam chạy ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 10 2023
a)Chọn gốc tọa độ tại A, chiều dương từ A đến B.
Phương trình chuyển động xe đi từ A: \(x_A=30t\left(km\right)\)
Phương trình chuyển động xe đi từ B: \(x_B=100-20t\left(km\right)\)
b)Hai xe gặp nhau: \(x_A=x_B\)
\(\Rightarrow30t=100-20t\Rightarrow t=2h\)
Nơi gặp cách A một đoạn: \(x_A=30\cdot2=60km\)
c)Tại lúc 9h, xe thứ nhất đi quãng đường: \(x_A=30\cdot1=30km\)
Và xe thứ hai đi quãng đường: \(x_B=100-20\cdot1=80km\)
Khi đó, hai xe cách nhau một đoạn:
\(\Delta x=x_B-x_A=80-30=50km\)
d)Thời điểm sau khi gặp nhau mà khoảng cách hai xe là 50km:
\(x_B-x_A=50\Rightarrow100-20t-30t=50\Rightarrow\) \(t=1h\)
VT
20 tháng 2 2019
Chọn đáp án C
Gọi vận tốc của hai xe lần lượt là v 1 , v 2
Khi hai xe chuyển động ngược chiều thì
Khi hai xe chuyển động cùng chiều thì
11 tháng 7 2017
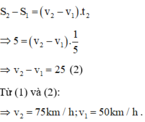
Gọi v1; v2 lần lượt là vận tốc 2 xe.
s1; s2 lần lượt là quãng đường 2 xe đi được trong 2 trường hợp.
Theo bài ra ta có:
\(s_1=\left(v_1+v_2\right)t=25\Rightarrow v_1+v_2=\dfrac{25}{0,25}=100\left(\text{km/h}\right)\left(1\right)\)
Giả sử v1 > v2:
\(s_2=\left(v_1-v_2\right)t=5\Rightarrow v_1-v_2=\dfrac{5}{0,25}=20\left(\text{km/h}\right)\left(2\right)\)
Lấy (1)+(2); ta có: \(2v_1=120\Rightarrow v_1=60\left(\text{km/h}\right)\Rightarrow v_2=40\left(\text{km/h}\right)\)
Vậy......................
25 tháng 9 2021
a,\(\Rightarrow\left\{{}\begin{matrix}xA=80t\\xB=200-40t\end{matrix}\right.\)\(\left(km,h\right)\)
b, gap nhau \(\Rightarrow xA=xB\Rightarrow t=\dfrac{5}{3}h\)
vi tri gap nhau cach A \(xA=\dfrac{400}{3}km\)
c,\(\Rightarrow d=\left|xA-xB\right|=\left|80.2-200+40.2\right|=40km\)
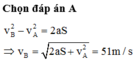
2 giờ đầu xe chạy đc quãng đường:
\(s_1=60.2=120\left(km\right)\)
3h sau xe chạy đc quãng đường:
\(s_2=40.3=120\left(km\right)\)
vận tốc trung bình của xe trong suốt thời gian chạy:
\(v_{tb}=\frac{s_1+s_2}{t_1+t_2}=\frac{120+120}{2+3}=48\left(km/h\right)\)