Chứng ninh rằng nếu 2 số có tích không thay đổi thì tổng nhỏ nhất của chúng xảy ra khi 2 số đó bằng nhau.
a.b=c (c là hằng số) => min(a+b) xảy ra khi a=b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 3 2023
3.1
Xét hiệu :
\(\left(\dfrac{a+b}{2}\right)^2-ab=\dfrac{a^2+2ab+b^2}{4}-\dfrac{4ab}{4}\)
\(=\dfrac{a^2-2ab+b^2}{4}=\dfrac{\left(a-b\right)^2}{4}\ge0\forall a,b\in R\)
Vậy \(\left(\dfrac{a+b}{2}\right)^2\ge ab,\forall a,b\in R\)
Dấu bằng xảy ra : \(\Leftrightarrow a=b\)
3.2
Áp dụng kết quả của câu 3.1 vào câu 3.2 ta được:
\(\left(a+b+c\right)^2=[a+\left(b+c\right)]^2\ge4a\left(b+c\right)\)
Mà : \(a+b+c=1\left(gt\right)\)
nên : \(1\ge4a\left(b+c\right)\)
\(\Leftrightarrow b+c\ge4a\left(b+c\right)^2\) ( vì a,b,c không âm nên b+c không âm )
Mà : \(\left(b+c\right)^2\ge4bc\Leftrightarrow\left(b-c\right)^2\ge0,\forall b,c\in N\)
\(\Rightarrow b+c\ge16abc\)
Dấu bằng xảy ra : \(\Leftrightarrow\left\{{}\begin{matrix}a=b+c\\b=c\end{matrix}\right.\Leftrightarrow b=c=\dfrac{1}{4};a=\dfrac{1}{2}\)
DK
12 tháng 5 2017
Bộ NST lưỡng bội là 2n.
Khi không xảy ra trao đổi chéo, số loại tinh trùng = 2n = 256 => n = 8.
Cặp NST trao đổi chéo tại 1 điểm => 4 loại tinh trùng.
Cặp NST trao đổi chéo tại 2 điểm không đồng thời => 6 loại tinh trùng
=> Số loại tinh trùng: 4 x 62 x 25 = 4608.
Chọn C.
10 tháng 3 2016
gọi xy=k^2 với k là hằng số.
Ta có: [(x+y)/2]^2 >=xy <=>(x+y)^2 >= 4xy <=> (x+y) >= 2k =>min(x+y)=2k<=>x=y=k.
10 tháng 3 2016
a)Xét hai số dương tích bằng a( với a là hằng số):
ta có (x+y)^2 >= 4xy=4a <=> x=y
Vì x,y >0 nên x+y nhỏ nhất <=> x=y.
BC
1
NB
27 tháng 1 2021
+Gọi 2 số đó là a, b \(\left(a,b>0\right)\)
+Có: a, b ko đổi
+Cần cm: \(\left(a+b\right)_{min}\Leftrightarrow a=b\)
+Có: \(\left(a-b\right)^2\ge0\\ \Rightarrow a^2-2ab+b^2\ge0\\ \Rightarrow a^2+b^2\ge2ab\\ \Rightarrow a^2+2ab+b^2\ge4ab\\ \Rightarrow\left(a+b\right)^2\ge4ab\\ \Rightarrow a+b\ge2\sqrt{ab}\)
Có: \(\left(a+b\right)_{min}=2\sqrt{ab}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-b\right)^2=0\\a+b=2\sqrt{ab}\end{matrix}\right.\)
\(\Leftrightarrow a=b=\sqrt{ab}\left(đpcm\right)\)
CM
19 tháng 11 2018
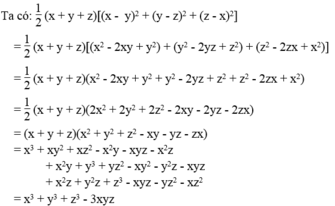
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :
DK
20 tháng 7 2018
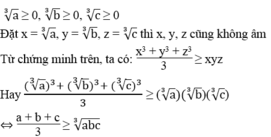
Chọn C
I đúng, vì 2 gen này được nhân đôi khi NST nhân đôi
II sai, phiên mã dựa vào nhu cầu của tế bào với sản phầm của 2 gen đó
III đúng
IV đúng