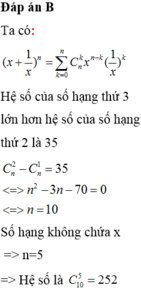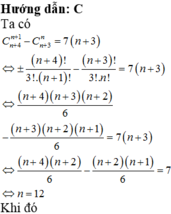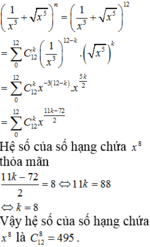tìm số mũ n trong khai triển của nhị thức \(\left(1+x\right)^n\)biết hệ số của số hạng thứ 5 và số hạng số 9 gằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 2
SHTQ của \(\left(3x+2\right)^5\) là \(C^k_5\cdot\left(3x\right)^{5-k}\cdot2^k=C^k_5\cdot3^{5-k}\cdot2^k\cdot x^{5-k}\)
Hệ số của số hạng chứa x tương ứng với 5-k=1
=>k=4
=>Hệ số là \(C^4_5\cdot3^{5-4}\cdot2^4=240\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021
Giả thiết tương đương:
\(C_{2n+1}^{n+1}+C_{2n+1}^{n+2}+...+C_{2n+1}^{2n}+C_{2n+1}^{2n+1}=2^{100}\) (thay \(1=C_{2n+1}^{2n+1}\))
Mặt khác:
\(C_{2n+1}^{2n+1}=C_{2n+1}^0\)
\(C_{2n+1}^{2n}=C_{2n+1}^1\)
....
\(C_{2n+1}^{n+1}=C_{2n+1}^n\)
Cộng vế:
\(\Rightarrow C_{2n+1}^{n+1}+C_{2n+1}^{n+2}+...+C_{2n+1}^{2n+1}=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^n\)
\(\Rightarrow2\left(C_{2n+1}^{n+1}+...+C_{2n+1}^{2n+1}\right)=C_{2n+1}^0+C_{2n+1}^1+...+C_{2n+1}^{2n+1}\)
\(\Rightarrow2.2^{100}=2^{2n+1}\) (đẳng thức cơ bản: \(\sum\limits^n_{k=0}C_n^k=2^n\))
\(\Leftrightarrow2^{101}=2^{2n+1}\)
\(\Rightarrow2n+1=101\)
\(\Rightarrow n=50\)
SHTQ trong khai triển: \(C_{50}^k.\left(x^{-3}\right)^k.\left(x^2\right)^{50-k}=C_{50}^kx^{100-5k}\)
\(100-5k=20\Rightarrow k=16\)
Hệ số: \(C_{50}^{16}\)