tìm x,y,z biết : x/y+z+1=y/x+z+1=z/x+y-2=x+y+z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
0
PH
0
KT
1
21 tháng 8 2015
\(\left(x-\frac{1}{2}\right)\left(y+\frac{1}{3}\right)\left(z-2\right)=0\) và \(x+2=y+3=z+4\)
\(\Rightarrow x-\frac{1}{2}=0\) hoặc \(y+\frac{1}{3}=0\) hoặc \(z-2=0\)
\(\Rightarrow x=\frac{1}{2}\) | \(y=-\frac{1}{3}\) | \(z=2\)
Khi \(x=\frac{1}{2}\) thì:
\(\frac{1}{2}+2=\frac{5}{2}\)
\(y=\frac{5}{2}-3=-\frac{1}{2}\)
\(z=\frac{5}{2}-4=\frac{-3}{2}\)
Khi \(y=\frac{-1}{3}\) thì:
\(\frac{-1}{3}+3=\frac{8}{3}\)
\(x=\frac{8}{3}-2=\frac{2}{3}\)
\(z=\frac{8}{3}-4=-\frac{4}{3}\)
Khi \(z=2\) thì:
\(2+4=6\)
\(x=6-2=4\)
\(y=6-3=3\)
Vậy (x,y,z) = \(\left(\frac{1}{2};-\frac{1}{2};-\frac{3}{2}\right)\) ; \(\left(\frac{2}{3};-\frac{1}{3};-\frac{4}{3}\right)\) ; \(\left(4;3;2\right)\)
14 tháng 10 2015
Ap dụng tính chất dãy tỉ số bằng nhau
: a/b = c/d = e/f = a+b+c/b+d+f có b+d+f \(\ne\)0
Ta xét trường hợp x+y+z = 0 có :
x/y+z+1= y/x+z+1 = z/(x+y-2) = 0 => x = y = z = 0
Ta xét x+y+z = 0, tính chất tỉ lệ thức:
x+y+z = x/y+z+1 = y/x+z+1 = z/x+y-2 = x+y+z/2x+2y+2z = 1/2
=> x+y+z = 1/2 và:
2x = y+z+1 = 1/2 - x + 1 => x = 1/2
2y = x+z+1 = 1/2 - y + 1 => y = 1/2
z = 1/2 - (x+y) = 1/2 - 1 = -1/2
Vậy có căp x,y,z thỏa mãn: 0,0,0 và 1/2,1/2,-1/2
LP
1
8 tháng 8 2016
\(x+y-y-z+z+x=\frac{1}{2}-\frac{1}{3}+\frac{1}{4}\)
\(\Rightarrow2x=\frac{5}{12}\)
\(\Rightarrow x=\frac{5}{12}:2\)
\(\Rightarrow x=\frac{5}{24}\)
Có x rồi bạn thế vào => ra được y rồi thế y vòa => được z
PT
1
CM
11 tháng 8 2018
Cộng theo từng vế các đẳng thức đã cho, ta được:
x.(x + y + z) + y(x + y + z) + z.(x+ y + z) = - 5 + 9 + 5
⇔ (x + y + z). (x + y + z ) = 9
Suy ra: (x + y + z)2 = 9 ⇒ x + y + z = ±3
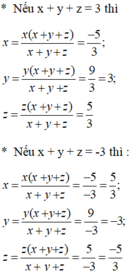
Ta có : \(\frac{x}{y+z+1}=\frac{y}{z+x+1}=\frac{z}{x+y-2}=x+y+z\) (1)
Áp dụng tính chất dãy tỉ số bằng nhau cho 3 đăng thức đầu tiên ta được :
\(\frac{x}{y+z+1}=\frac{y}{z+x+1}=\frac{z}{x+y-2}=\frac{x+y+z}{y+z+1+x+z+1+x+y-2}=\frac{x+y+z}{2.\left(x+y+x\right)}=\frac{1}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\frac{1}{2}=x+y+z\) và \(\left\{{}\begin{matrix}2x=y+z+1\\2y=z+x+1\\2z=x+y-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-1=\frac{1}{2}\\3y-1=\frac{1}{2}\\3z+2=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{1}{2}\\y=\frac{1}{2}\\z=-\frac{1}{2}\end{matrix}\right.\)
Vậy : ....