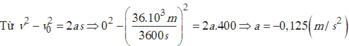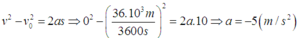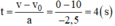Một xe máy đang đi bỗng người lái xe thấy có một cái hố trước mặt, miệng hố cách xe 20m. Người đó phanh gấp và xe đến sát miệng hố thì dừng lại. Biết xe chuyển động chậm dần đều với gia tốc 2,5m/s^2. Tìm vận tốc ban đầu của xe và thời gian giảm phanh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 10 2021
\(v_0=36km\)/h\(=10m\)/s
Gia tốc xe: \(v^2-v_0^2=2aS\Rightarrow a=\dfrac{0^2-10^2}{2\cdot20}=-2,5m\)/s2
Thời gian hãm phanh: \(v=v_0+at\Rightarrow0=10-2,5\cdot t\Rightarrow t=4s\)
VT
29 tháng 4 2017
Ta có: ban đầu xe có v0 = 36 km/h = 10 m/s
Sau đó xe hãm phanh, sau quãng đường S = 20 m xe dừng lại: v = 0
Gia tốc của xe là:
1 tháng 7 2016
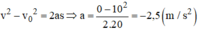
Tóm tắt:
Vo=30km/h=10m/s
S=20m
V=0
a) Chọn trục ox trùng với quỹ đạo chuyển động thẳng của xe, chiều dương hướng theo chiều chuyển động, mốc thời gian là lúc xe bắt đầu hãm phanh. Công thức liên hệ giữa quãng đường đi được với gia tốc và vận tốc bằng:
V^2 - Vo^2= 2aS
<=> -100=2a.20
<=>a=-2,5 (m/s^2)
b) Thời gian hãm phanh:
Ta có: a=(V-Vo)/t
<=>t=(V-Vo)/a
<=>t=(0-10)/(-2,5)
<=>t=4 (s)
1 tháng 7 2016
ta có v0 = 36 km/h = 10m/s ; v = o; s = 20m
a) Áp dụng công thức 2as = v2 - v02
=> a = =
= -2,5 m/s2.
b) Áp dụng công thức v = v0 + at
=> t =
=> t = = 4 s
=> t = 4 s.