Áp dụng HDT
4x2 -9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
2 tháng 4 2018
4x2 – 4x + 1 = 0;
a = 4; b = -4; c = 1
Δ = b2 - 4ac = (-4)2 - 4.4.1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
CM
4 tháng 11 2017
a) 5 x 2 – x + 2 = 0 ;
a = 5; b = -1; c = 2
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 5 . 2
= 1 - 40 = -39 < 0
Vậy phương trình trên vô nghiệm.
b) 4 x 2 – 4 x + 1 = 0 ;
a = 4; b = -4; c = 1
Δ = b 2 - 4 a c = ( - 4 ) 2 - 4 . 4 . 1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
c) - 3 x 2 + x + 5 = 0
a = -3; b = 1; c = 5
Δ = b 2 - 4 a c = 12 - 4 . ( - 3 ) . 5 = 1 + 60 = 61 > 0
⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt
x 1 = ( 1 - √ 61 ) / 6 ; x 2 = ( 1 + √ 61 ) / 6
TT
1
26 tháng 2 2022
Bài 2:
a: \(=\dfrac{4x^2+3-19}{x-2}=\dfrac{4x^2-16}{x-2}=\dfrac{4\left(x-2\right)\left(x+2\right)}{x-2}=4x+8\)
b: \(=\dfrac{2x}{x^2+2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)
\(=\dfrac{2}{x+2y}-\dfrac{1}{x-2y}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2x-4y-x-2y+4}{\left(x+2y\right)\left(x-2y\right)}\)
\(=\dfrac{x-6y+4}{\left(x+2y\right)\left(x-2y\right)}\)
CM
20 tháng 8 2019
Ta có:
f(x) = x4 – x2 + 6x – 9 = x4 – (x2 – 6x +9) = – (x-3)2
= (x2 –x + 3).(x2 + x - 3)
+ Tam thức x2 – x + 3 có Δ = -11 < 0, a = 1 > 0 nên x2 – x + 3 > 0 với ∀ x ∈ R.
+ Tam thức x2 + x – 3 có hai nghiệm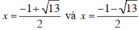 
Ta có bảng xét dấu sau:
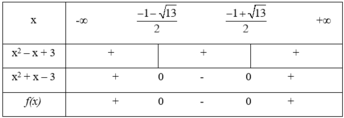
Kết luận:
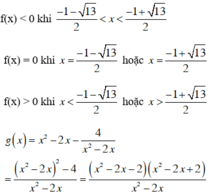
Tam thức x2 - 2x + 2 có Δ = -4 < 0, hệ số a = 1 > 0 nên x2 - 2x + 2 > 0 với ∀ x ∈ R
Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3.
Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2
Ta có bảng xét dấu :
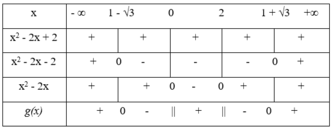
Kết luận : g(x) < 0 khi x ∈ (1 - √3; 0) ∪ (2; 1 + √3)
g(x) = 0 khi x = 1- √3 hoặc x = 1 + √3
g(x) > 0 khi x ∈ (-∞; 1 - √3) ∪ (0; 2) ∪ (1 + √3; +∞)
g(x) không xác định khi x = 0 và x = 2.
PT
1
26 tháng 10 2021
\(\Leftrightarrow M\cdot\left(4x^2+2x-9\right)=\left(4x^2+2x-18-4x^2-2x\right)\left(4x^2+2x-18+4x^2+2x\right)\)
\(\Leftrightarrow M\cdot\left(4x^2+2x-9\right)=-18\cdot\left(8x^2+4x-18\right)\)
\(\Leftrightarrow M=-18\cdot2=-36\)
4x2 - 9
= ( 2x)2 - 32
= ( 2x - 3 )( 2x + 3 )
Chak v :p
\(4x^2-9\)
\(=\left(2x\right)^2-3^2\)
\(=\left(2x-3\right)\left(2x+3\right)\)