Chứng minh rằng nếu m; n là các sô tự nhiên thoả mãn 4m2+m=5n2+n thì
(m-n) và (5m+5n+1) đều là số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
25 tháng 5 2023
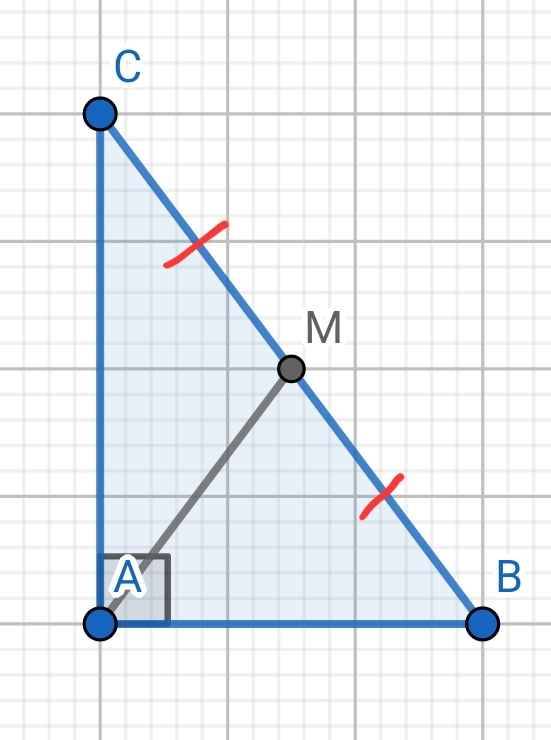
a) ∆ABC vuông tại A
M là trung điểm BC
⇒ AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
b) ∆ABC vuông tại A có ∠C = 30⁰
⇒ ∠B = 90⁰ - 30⁰ = 60⁰
Do AM = BM (cmt)
⇒ ∆ABM cân tại M
Lại có ∠ABM = ∠B = 60⁰
⇒ ∆ABM đều
⇒ AB = AM = BM = BC : 2
29 tháng 11 2021
\(4,VT=-a+b+c-a+b-c+a-b-c=-a+b-c=-\left(a-b+c\right)=VP\\ 5,M=-a+b-b-c+a+c-a=-a\\ M>0\Rightarrow-a>0\Rightarrow a< 0\)
KN
1
ND
Nguyễn Đức Trí
VIP
27 tháng 7 2023
vì khi \(a=1\Rightarrow a^4+4a=1^5+4.1=5\) (là số nguyên tố)
\(\Rightarrow m\ne5\Rightarrow a^4+4a\ne5\Rightarrow a\left(a^3+4\right)\ne5\Rightarrow a\ne1\left(a\in Z\right)\)
mà \(\left\{{}\begin{matrix}a^4⋮n\left(a\ne1\Rightarrow n\ne1;n\in Z\right)\\4a⋮4\&a\end{matrix}\right.\)
\(\Rightarrow a^4+4a\) không là số nguyên tố
3 tháng 9 2021
a: Gọi D là điểm đối xứng của A qua M
Xét tứ giác ABDC có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AD
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AD=BC
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)
PN
4
LP
7 tháng 4 2015
a/b<1=>a<b
Muốn chứng minh /b<a+m/b+m ta phải chứng minh a(b+m)<b(a+m)
Ta có:a.(b+m)=ab+am
b.(a+m)=ba+bm
vì a<b=>am<bm
Vậy a/b<a+m/b+m
TV
1
25 tháng 2 2021
`a vdots m,b vdots m`
`=>a+b vdots m`
Mà `a+b+c vdots m`
`=>a+b+c-(a+b) vdots m`
`=>a+b+c-a-b vdots m`
`=>(a-a)+(b-b)+c vdots m`
`=>0+0+c vdots m`
`=>c vdots m(forall a,b,c in Z)`
8 tháng 5 2021
Chỉ có thể đưa ra ví dụ thôi chứ đây đã là kiến thức cơ bản r nhé bn.
12 tháng 10 2021
Áp dụng công thức
- Tất cả các số trong 1 tổng đều chia hết cho cùng 1 số thì cả tổng đó sẽ chia hết cho số đó , chỉ cần 1 số ko chia hết thì cả tổng đó cũng sẽ ko chia hết
TT
0