Cho \(\Delta\)ABC vuông tại A, đường cao AH. D và E lần lượt là hình chiếu của H trên AB, AC. Qua D và E kẻ các đường thẳng vuông góc với DE lần lượt cắt BC tại M, N.
a, Chứng minh AB.AD=AE.AC
b, Chứng minh AD.BD+AE.EC=AH2
c, Chứng minh M, N lần lượt là trung điểm của BH, CH
d, Chứng minh \(\frac{CE}{BD}=\frac{AC^3}{AB^3}\)
e, Chứng minh \(\sqrt[3]{BC^2}=\sqrt[3]{BD^2}+\sqrt[3]{CE^2}\)
Ai biết bài này làm ơn giải giúp mình câu e với, các câu còn lại mình làm được rồi. Cám ơn trước nha!




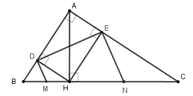
câu b làm kiểu gì vậy ạ?
Câu b: Tam giác AHB vuông tại H, đường cao AH
=> AD.BD=DH2
Tương tự: AE.EC=HE2
=> AD.BD+AE.EC=DH2+HE2
=DE2 (Pytago)
=AH2 (ADHE là hình chữ nhật vì có 3 góc vuông)