1 Chứng minh đẳng thức
12 8.912=1816
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 11 2017
128.912 = 1816
Ta có: 128.912 = (4.3)8.912 =48.38.912 =(22)8.(32)4.912
= 216.94.912 = 216.916= (2.9)16 = 1816
Vế trái bằng vế phải nên đẳng thức được chứng minh
CM
10 tháng 8 2019
Đặt vế trái bằng S n . Kiểm tra với n = 1 hệ thức đúng.
Giả sử đã có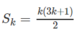 
với k ≥ 1.
Ta phải chứng minh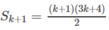 
Thật vậy
CM
15 tháng 3 2017
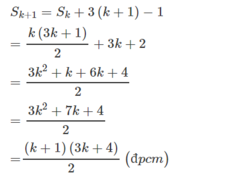
+ Với n = 1, ta có:
VT = 3 – 1 = 2
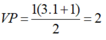
⇒ VT = VP
⇒ (1) đúng với n = 1
+ Giả sử (1) đúng với n = k ≥ 1 nghĩa là:
2 + 5 + 8 + …+ (3k – 1) = k(3k + 1)/2. (*)
Ta cần chứng minh (1) đúng với n = k + 1, tức là :
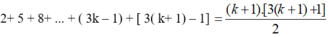
Thật vậy :
Ta có :
CM
17 tháng 6 2019
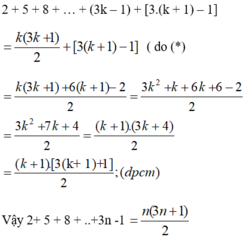
Ta có:
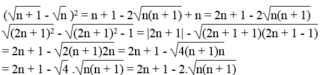
Vế trái bằng vế phải nên đẳng thức được chứng minh.
* Với n = 1, ta có: 2 - 1 2 = 9 - 8
* Với n = 2, ta có: 3 - 2 2 = 25 - 24
* Với n = 3, ta có: 4 - 3 2 = 49 - 48
* Với n = 4, ta có: 5 - 4 2 = 81 - 80
CM
8 tháng 8 2018
Kiểm tra với n = 1
Giả sử đã cho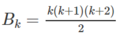 
Ta cần chứng minh
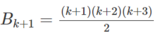
bằng cách tính
CM
10 tháng 9 2017
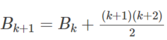
Đặt vế trái bằng S n
Với n = 1 vế trái chỉ có một số hạng bằng 1, vế phải bằng 1
Giả sử đã có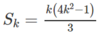 
với k ≥ 1. Ta phải chứng minh
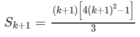
Thật vậy, ta có
S k + 1 = S k + 2 k + 1 - 1 2 = S k + 2 k + 1 2
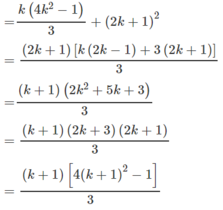
\(12^8\cdot9^{12}\)
\(=\left(2^2\cdot3\right)^8\cdot\left(3^2\right)^{12}\)
\(=\left(2^2\right)^8\cdot3^8\cdot3^{24}\)
\(=2^{16}\cdot3^{32}\)
\(=2^{16}\cdot\left(3^2\right)^{16}\)
\(=\left(2\cdot3^2\right)^{16}\)
\(=18^{16}\)