cho tam giác ABC sao cho có G là trọng tâm . Gọi H là chân đường đường cao hạ từ A sao cho \(\overrightarrow{BH}=\frac{1}{3}\overrightarrow{HC}\), Điểm M di động nằm trên BC sao cho \(\overrightarrow{BM}=x\overrightarrow{BC}\) . tìm x sao cho độ dài của vecto \(\overrightarrow{MA}+\overrightarrow{GC}\) đạt giá trị nhỏ nhất .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 10 2020
Gọi A là trọng tâm tam giác ABC. AB = GB-GA = ỊmB-|kA 3 3 = |(AK-BM) = |(Ó-Ĩ) Ta có BC = GC - GB = (-GA - GB) - GB =-GA-2GB = AG + 2BG Chú ý: A là trọng tâm AABC thì GA + AB + AC = õ.
21 tháng 1 2020
Dựng hình bình hành \(AGCE\). Ta có: \(\overrightarrow{MA}+\overrightarrow{GC}=\overrightarrow{MA}+\overrightarrow{AE}=\overrightarrow{ME}\)
Kẻ \(EF\perp BC\left(F\in BC\right)\). Khi đó: \(\left|\overrightarrow{MA}+\overrightarrow{GC}\right|=\left|\overrightarrow{ME}\right|=ME\ge EF\)
Do đó: \(\left|\overrightarrow{MA}+\overrightarrow{GC}\right|\) nhỏ nhất khi \(M\equiv F\)
Gọi \(P\) là trung điểm \(AC,Q\) là hình chiếu vuông góc của \(P\) lên
Khi đó \(P\) là trung điểm \(GE\) nên \(BP = \dfrac{3}{4}BE \)
Ta có: \(\Delta BPQ\sim\Delta BEF\Rightarrow\)\(\dfrac{{BQ}}{{BF}} = \dfrac{{BP}}{{BE}} = \dfrac{3}{4}\) hay \(\overrightarrow {BF} = \dfrac{4}{3}\overrightarrow {BQ} \)
Mặt khác, \(\overrightarrow {BH} = \dfrac{1}{3}\overrightarrow {HC} \)
$PQ$ là đường trung bình \(\Delta AHC\) nên $Q$ là trung điểm $HC$ hay \(\overrightarrow {HQ} = \dfrac{1}{2}\overrightarrow {HC} \)
Suy ra: \(\overrightarrow {BQ} = \overrightarrow {BH} + \overrightarrow {HQ} = \dfrac{1}{3}\overrightarrow {HC} + \dfrac{1}{2}\overrightarrow {HC} = \dfrac{5}{6}\overrightarrow {HC} = \dfrac{5}{6}.\dfrac{3}{4}\overrightarrow {BC} = \dfrac{5}{8}\overrightarrow {BC} \)
Do đó: \(\overrightarrow {BF} = \dfrac{4}{3}\overrightarrow {BQ} = \dfrac{5}{6}\overrightarrow {BC} \)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 10 2020
\(\overrightarrow{GB}=-\frac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{BC}\right)=\frac{1}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{BC}\)
\(=\frac{1}{3}\overrightarrow{AH}+\frac{1}{3}\overrightarrow{HB}-\frac{1}{3}\overrightarrow{BC}=\frac{1}{3}\overrightarrow{AH}+\frac{1}{3}.\frac{3}{4}\overrightarrow{BC}-\frac{1}{3}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{GB}=\frac{1}{3}\overrightarrow{AH}-\frac{1}{12}\overrightarrow{BC}\)
\(\overrightarrow{MA}=\overrightarrow{MH}+\overrightarrow{HA}=\left(\frac{1}{4}-x\right)\overrightarrow{BC}-\overrightarrow{AH}\)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{GB}=\left(\frac{1}{3}-x\right)\overrightarrow{BC}-\frac{2}{3}\overrightarrow{AH}\)
Đặt \(T=\left|\overrightarrow{MA}+\overrightarrow{GB}\right|=\left|\left(\frac{1}{3}-x\right)\overrightarrow{BC}-\frac{2}{3}\overrightarrow{AH}\right|\)
\(\Rightarrow T^2=\left(\frac{1}{3}-x\right)^2.BC^2+\frac{4}{9}AH^2\ge\frac{4}{9}AH^2\)
Dấu "=" xảy ra khi \(\frac{1}{3}-x=0\Leftrightarrow x=\frac{1}{3}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OF} } \right)\)
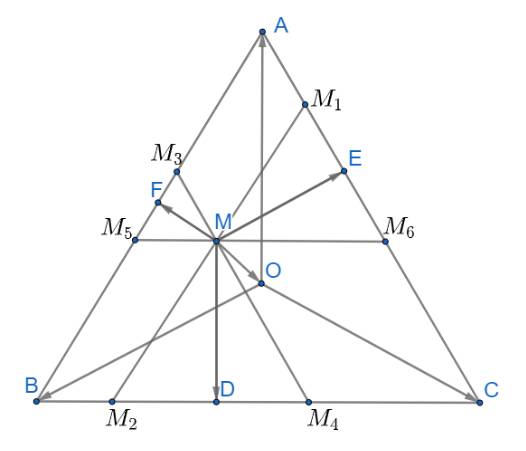
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\)
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = 60^\circ \)
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều
Áp dụng tính chất trung tuyến \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)(với M là trung điểm của BC) ta có:
\(\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
Ta có: các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành
Áp dụng quy tắc hình bình hành ta có
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} + \overrightarrow {M{M_6}} } \right)\)
\( = \frac{1}{2}\overrightarrow {MA} + \frac{1}{2}\overrightarrow {MB} + \frac{1}{2}\overrightarrow {MC} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right) = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
