Cho tứ giác ABCD có AC cắt BD tại O
CM: a) 2BO > AB+BC-AC
b) Nếu AB + BD < AC + CD thì AB < AC
c) Nếu AC \(\perp\) BD thì \(AB^2+CD^2=BC^2+AD^2\)
HELP ME
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NB
1
DD
Đoàn Đức Hà
Giáo viên
23 tháng 6 2021
a) Gọi \(O\)là giao điểm \(AC\)và \(BD\).
Theo bất đẳng thức tam giác ta có:
\(OA+OB>AB,OB+OC>BC,OC+OD>CD,OD+OA>AD\)
Cộng lại vế theo vế ta được:
\(2\left(OA+OB+OC+OD\right)>AB+BC+CD+DA\)
\(\Leftrightarrow AC+BD>\frac{1}{2}\left(AB+BC+CD+DA\right)\).
b) Theo bất đẳng thức tam giác:
\(AC< AB+BC,AC< CD+DA,BD< AB+DA,BD< BC+CD\)
Cộng lại vế theo vế ta được:
\(2\left(AC+BD\right)< 2\left(AB+BC+CD+DA\right)\)
\(\Leftrightarrow AC+BD< AB+BC+CD+DA\).
CM
16 tháng 6 2018
Ta có: A B → . C D → = A C → . B D → = A D → . C B → = 0
⇒ A B → ( A D → - A C → ) = A C → ( A D → - A B → ) = A D → ( A B → - A C → ) = 0
⇒ A B → . A C → = A C → . A D → = A B → . A D →
Đáp án C
6 tháng 7 2023
Gọi giao của AB và CD là O
a: AB vuông góc CD
AC^2-BC^2
=AO^2+OC^2-CO^2-BO^2
=AO^2-BO^2
=AO^2+OD^2-OD^2-OB^2
=AD^2-BD^2
b: AC^2-BC^2=AD^2-BD^2
=>AC^2-AD^2=BC^2-BD^2
=>(vecto AC)^2-(vecto AD)^2=(vecto BC)^2-(vecto BD)^2
=>(vecto AC-vecto AD)(vecto AC+vecto AD)=(vecto BC-vecto BD)(vecto BC+vecto BD)
=>vecto DC*vecto AM*2=vecto DC*vecto BM*2(M là trung điểm của DC)
=>vecto DC*vecto AB=0
=>DC vuông góc AB
PT
1
CM
16 tháng 8 2019
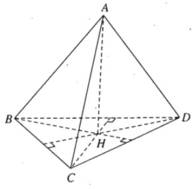
Vẽ AH ⊥ (BCD) tại H, ta có CD ⊥ AH và vì CD ⊥ AB ta suy ra CD ⊥ BH. Tương tự vì BD ⊥ AC ta suy ra BD ⊥ CH
Vậy H là trực tâm của tam giác BCD tức là DH ⊥ BC
Vì AH ⊥ BC nên ta suy ra BC ⊥ AD
Cách khác: Trước hết ta hãy chứng minh hệ thức:
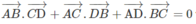
với bốn điểm A, B, C, D bất kì.
Thực vậy , ta có:
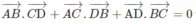
Do đó nếu AB ⊥ CD nghĩa là
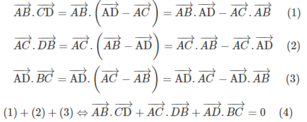
Từ hệ thức (4) ta suy ra
,
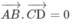do đó AD ⊥ BC.