cho hình bình hành abcd có ab>bc . đường phân giác của góc d cắt ab tại m đường phân giác góc b cắt cd tại n
a, chuwnngs minh am =cn
b, chưng minh tú giác dmbc là hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN

a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN

a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=CB
\(\widehat{A}=\widehat{C}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN
phần c em để chữ đậm đó ạ chứ phần a em làm cách khác rồi, em cảm ơn ạ

a) Ta có :
\(\hept{\begin{cases}NE\perp DM\\MG\perp BN\end{cases}}\)
\(\Rightarrow DM//BN\)
\(\Rightarrow\widehat{EDN}=\widehat{GBM}\)( sole trong) (1)
Mà \(\widehat{ADE}=\widehat{EDN}\)(2)
Từ (1) và(2)
\(\Rightarrow\widehat{ADE}=\widehat{GBM}\)
Lại có : \(DM//BN\left(cmt\right)\)
\(\Rightarrow\widehat{AMD}=\widehat{GBM}\)
\(\Rightarrow\widehat{ADM}=\widehat{AMD}\)
=> Tam giác ADM cân tại A
\(\Rightarrow AM=AD\left(dpcm\right)\)
b) P/s: phải là chứng minh tam giác MGB và tam giác NED chớ không phải tam giác MHB bạn ơi .
giải : Xét \(\Delta MGB\)và \(\Delta NED\)ta có :
\(MB=DN\)
\(\widehat{E}=\widehat{G}=90^o\)
\(\widehat{EDN}=\widehat{GBM}\)( câu a )
=> \(\Delta MGB=\Delta NED\)( cạnh huyền - góc nhọn )
c) Vì ABCD là hình bình hành
\(\Rightarrow BM//DN\)( vì AB // CD ) (1)
Lại có : \(DM//BN\)( câu a ) (2)
Từ (1)và(2)
=> MBND là hình bình hành (đpcm)

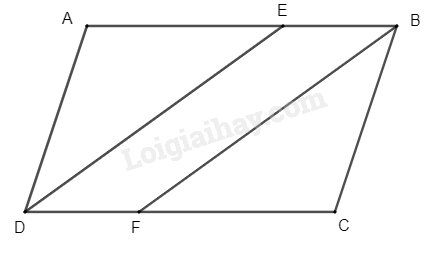
a) Vì \(DE\), \(BF\) là phân giác (gt)
Suy ra \(\widehat {{\rm{ADE}}} = \widehat {{\rm{EDC}}} = \frac{{\widehat {ADC}}}{2}\); \(\widehat {{\rm{EBF}}} = \widehat {{\rm{CBF}}} = \frac{{\widehat {ABC}}}{2}\) (1)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\) và \(\widehat {ADC} = \widehat {ABC}\) (2)
Suy ra \(\widehat {{\rm{AED}}} = \widehat {{\rm{EDC}}}\) (so le trong) (3)
Từ (1), (2), (3) suy ra \(\widehat {AED} = \widehat {ABF}\)
Mà hai góc ở vị trí đồng vị
Suy ra \(DE\) // \(BF\)
b) Xét tứ giác \(DEBF\) ta có:
\(DE\) // \(BF\) (cmt)
\(BE\) // \(DF\) (do \(AB\) // \(CD\))
Suy ra \(DEBF\) là hình bình hành
giúp mình với ạ