cho tam giác đều ABC có cạnh bằng a ,H là trung điểm của BC.Vecto CH + vecto CH có độ dài là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|\overrightarrow{AM}\right|=AM=\dfrac{a\sqrt{3}}{2}\)

ΔABC đều có BM là đường trung tuyến
nên BM là phân giác của góc ABC và BM\(\perp\)AC
BM là phân giác của góc ABC
=>\(\widehat{ABM}=\widehat{CBM}=\dfrac{\widehat{ABC}}{2}=30^0\)
M là trung điểm của AC
=>\(AM=MC=\dfrac{AC}{2}=\dfrac{a}{2}\)
ΔAMB vuông tại M
=>\(AM^2+BM^2=AB^2\)
=>\(BM^2=AB^2-AM^2=a^2-\left(0,5a\right)^2=0,75a^2\)
=>\(BM=\dfrac{a\sqrt{3}}{2}\)
Gọi K là trung điểm của AM
=>\(KA=KM=\dfrac{AM}{2}=0,25a\)
ΔBMK vuông tại M
=>\(BM^2+MK^2=BK^2\)
=>\(BK^2=\left(0,25a\right)^2+\left(\dfrac{a\sqrt{3}}{2}\right)^2=\dfrac{13}{16}a^2\)
=>\(BK=\dfrac{a\sqrt{13}}{4}\)
Xét ΔBAM có BK là đường trung tuyến
nên \(\overrightarrow{BA}+\overrightarrow{BM}=2\cdot\overrightarrow{BK}\)
=>\(\left|\overrightarrow{BA}+\overrightarrow{BM}\right|=2\cdot BK=2\cdot\dfrac{a\sqrt{13}}{4}=\dfrac{a\sqrt{13}}{2}\)

Lời giải:
\(\overrightarrow{AC}.\overrightarrow{BI}=(\overrightarrow{AM}+\overrightarrow{MC})(\overrightarrow{BM}+\overrightarrow{MI})\)
\(=\overrightarrow{AM}.\overrightarrow{BM}+\overrightarrow{AM}.\overrightarrow{MI}+\overrightarrow{MC}.\overrightarrow{BM}+\overrightarrow{MC}.\overrightarrow{MI}\)
\(=\overrightarrow{AM}.\overrightarrow{MI}+\overrightarrow{MC}.\overrightarrow{BM}\)
\(=\overrightarrow{AM}.\frac{-\overrightarrow{AM}}{2}+\frac{\overrightarrow{BC}}{2}.\overrightarrow{BC}=\frac{BC^2-AM^2}{2}\)
\(=\frac{BC^2-(\frac{\sqrt{3}}{2}BC)^2}{2}=\frac{BC^2}{8}=\frac{9a^2}{8}\)
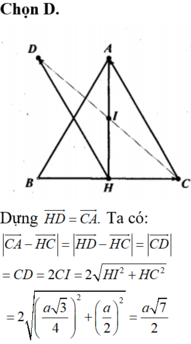
\(\left|\overrightarrow{CH}+\overrightarrow{CH}\right|=a\)