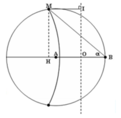
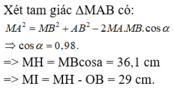Hai nguồn kết hợp A và B cách nhau 16cm dao động cùng pha nhau với tần số f=100Hz, vận tốc truyền sóng bằng 1m/s. Bao quanh A và B bằng một vòng tròn tâm O nằm tại trung điểm AB với bán kính R=4cm. Số vân lồi cắt nửa vòng nằm về 1 phía của AB là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
22 tháng 12 2019
chọn đáp án A
λ
=
3
c
m
Số điểm dao động cực đại trên đoạn AB thoả trong khoảng
-
A
B
λ
≤
k
≤
A
B
λ
⇒
-
6
,
6
≤
k
≤
6
,
6
Dễ dàng nhận thấy điểm M dao động với biên độ cực đại xa đường trung trực nhất nằm ở vân -6 là giao của vân cực đại bậc -6 gần A nhất với đường tròn.Gọi O là trung điểm của AB H là hình chiếu của M trên đường thẳng AB,d là khoảng cách từ M đến trung trực
M H = h , A H = O H - A O = d - 10 , B H = B O + O H = d + 10 A M = d 1 , B M = d 2 t a c ó : d 1 - d 2 = - 6 λ ⇒ - 18 ⇒ d 2 = 38 d o d 1 = A B = 20 ⇒ M H 2 = M A 2 - A H 2 = M B 2 - B H 2 ⇒ h 2 = d 1 2 - ( d - 10 ) 2 = d 2 2 - ( d + 10 ) 2
-> d=26,1
VT
18 tháng 3 2018
Đáp án A
λ
=
3
c
m
Số điểm dao động cực đại trên đoạn AB thoả trong khoảng
-
A
B
λ
≤
k
A
B
λ
⇒
-
6
,
6
≤
k
≤
6
,
6
Dễ dàng nhận thấy điểm M dao động với biên độ cực đại xa đường trung trực nhất nằm ở vân -6 là giao của vân cực đại bậc -6 gần A nhất với đường tròn.Gọi O là trung điểm của AB H là hình chiếu của M trên đường thẳng AB,d là khoảng cách từ M đến trung trực
MH = h, AH=OH-AO=d-10,
BH=BO+OH=d+10
AM= d 1 ,
BM= d 1 .
ta có d 1 - d 2 = - 6 λ ⇒ - 18 ⇒ d 2 = 38
do d 1 = A B = 20
M H 2 = M A 2 - A H 2 = M B 2 - B H 2
⇒ h 2 = d 1 2 - ( d - 10 ) 2 = d 2 2 - ( d + 10 ) 2
⇒ d = 26 , 1
VT
3 tháng 8 2018
Chọn D.
Xét A B λ = 6,67
Nếu M là cực tiểu xa đường trung trực nhất (gần A nhất) thì
MA-MB = 6,5 λ => MB = 39,5 (cm)
Xét tam giác MAB:
VT
10 tháng 6 2019
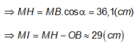
Đáp án A
gọi M là điểm nằm trên đường tròn tâm A bán kính AB, M cực đại => d1 -d2 = k lamda
mà điểm M nằm trên dãy cực đại gần đường trung trực nhất nên k = 1
=> d2 = 17 cm
=> khoảng cách từ M đến đường trung trực là x
ta có d2^2 - (AB/2 + x)^2 = d1^2 - (AB/2 -x)^2
=> x = 27,75 mm
VT
11 tháng 7 2018
chọn đáp án C
Điểm trên đường tròn dao đọng với biên độ cực đại cách trung trực của AB gần nhất, tức là gần nhất ứng với đường k=0
=>Điểm đó nằm trên đường k=
±
1
Trường hợp k = 1
Suy ra MB=MA=
λ
<=> MB-20=3 <=> MB = 23 cm
Gọi N là hình chiếu của M xuống AB, ta có
A
M
2
-
A
N
2
=
M
N
2
=
B
M
2
-
B
N
2
Vậy ta có hệ phương trình
B
N
2
-
A
N
2
=
B
M
2
-
A
M
2
=
129
B
N
+
A
N
=
A
B
=
20
Giải hệ trên ta được AN = 6.775, vây khoảng cách là 10-6.775=3.225
Trường hợp k = -1
Suy ra MB-MA=
-
λ
<=> MB-20=-3 <=> MB=17cm
Gọi N là hình chiếu của M xuống AB, ta có
A
M
2
-
A
N
2
=
M
N
2
=
B
M
2
-
B
N
2
Vậy ta có hệ phương trình
B
N
2
-
A
N
2
=
B
M
2
-
A
M
2
=
-
111
B
N
+
A
N
=
A
B
=
20
Giải hệ trên ta được AN = 12.775, vây khoảng cách là 12.775-10=2.775