cho tứ giác ABCD có AB=AD,BC=CD. Chứng minh rằng ;
a)B và D đối xứng với nhau qua AC
b)Tứ giác ABCD là hình có trục đối xứng
giúp mình với mình cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác ABCD có
AB//CD
AD//BC
DO đó: ABCD là hình bình hành
Suy ra: AB=CD; AD=BC


1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
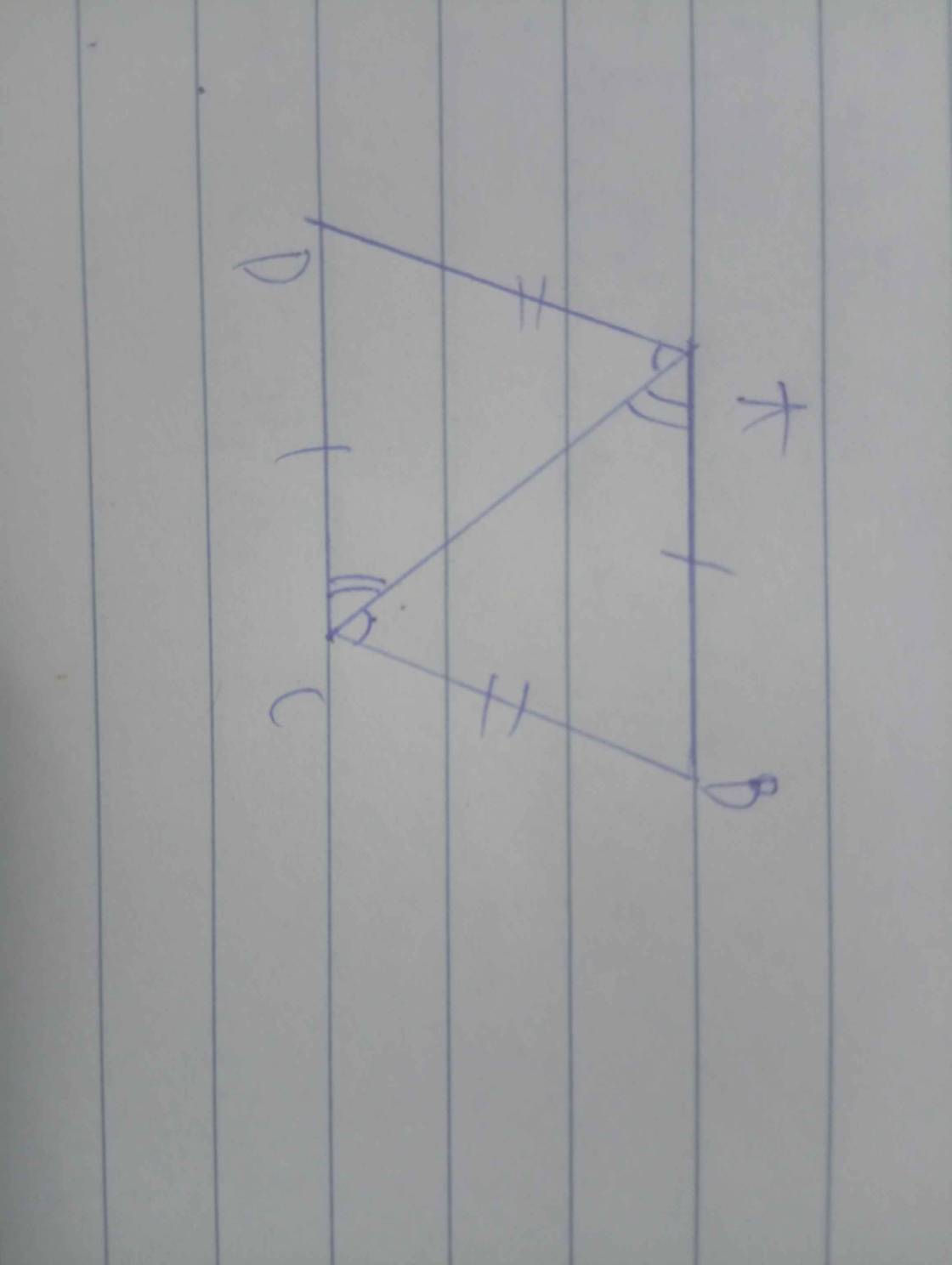

Giả sử tứ giác ABCD là hình thang ( AB // CD)
Xét hình thang ABCD ta có:
E là trung điểm AD (gt)
F là trung điểm BC (gt)
=> EF là đường trung bình của hình thang ABCD
=> EF = ( AB + CD)/2
Vậy tứ giác ABCD là hình thang ( AB // CD) thì EF = ( AB + CD)/2
Giả sử tứ giác ABCD là hình thang ( AB // CD)
Xét hình thang ABCD ta có:
E là trung điểm AD (gt)
F là trung điểm BC (gt)
=> EF là đường trung bình của hình thang ABCD
=> EF = ( AB + CD)/2
Vậy tứ giác ABCD là hình thang ( AB // CD) thì EF = ( AB + CD)/2
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~
a: Ta có: AB=AD
nên A nằm trên đường trung trực của BD(1)
ta có: BC=CD
nên C nằm trên đường trung trực của BD(2)
Từ (1) và (2) suy ra BD là đường trung trực của AC
hay A và C đối xứng nhau qua BD