Cho a, b, c \(\inℕ^∗\)và a2 = b2 + c2. CM : abc chia hết cho 60.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: a+b+c=0
nên a+b=-c
Ta có: \(a^2-b^2-c^2\)
\(=a^2-\left(b^2+c^2\right)\)
\(=a^2-\left[\left(b+c\right)^2-2bc\right]\)
\(=a^2-\left(b+c\right)^2+2bc\)
\(=\left(a-b-c\right)\left(a+b+c\right)+2bc\)
\(=2bc\)
Ta có: \(b^2-c^2-a^2\)
\(=b^2-\left(c^2+a^2\right)\)
\(=b^2-\left[\left(c+a\right)^2-2ca\right]\)
\(=b^2-\left(c+a\right)^2+2ca\)
\(=\left(b-c-a\right)\left(b+c+a\right)+2ca\)
\(=2ac\)
Ta có: \(c^2-a^2-b^2\)
\(=c^2-\left(a^2+b^2\right)\)
\(=c^2-\left[\left(a+b\right)^2-2ab\right]\)
\(=c^2-\left(a+b\right)^2+2ab\)
\(=\left(c-a-b\right)\left(c+a+b\right)+2ab\)
\(=2ab\)
Ta có: \(M=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
\(=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
\(=\dfrac{a^3+b^3+c^3}{2abc}\)
Ta có: \(a^3+b^3+c^3\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ca-cb+c^2\right)-3ab\left(a+b\right)\)
\(=-3ab\left(a+b\right)\)
Thay \(a^3+b^3+c^3=-3ab\left(a+b\right)\) vào biểu thức \(=\dfrac{a^3+b^3+c^3}{2abc}\), ta được:
\(M=\dfrac{-3ab\left(a+b\right)}{2abc}=\dfrac{-3\left(a+b\right)}{2c}\)
\(=\dfrac{-3\cdot\left(-c\right)}{2c}=\dfrac{3c}{2c}=\dfrac{3}{2}\)
Vậy: \(M=\dfrac{3}{2}\)

Ta có: \(a\left(b^2-1\right)\left(c^2-1\right)+b\left(a^2-1\right)\left(c^2-1\right)+c\left(a^2-1\right)\left(b^2-1\right)\)
\(=a\left(b^2c^2-b^2-c^2+1\right)+b\left(a^2c^2-a^2-c^2+1\right)\)
\(+c\left(a^2b^2-a^2-b^2+1\right)\)
\(=ab^2c^2-ab^2-ac^2+a+ba^2c^2-a^2b-bc^2+b\)
\(+ca^2b^2-a^2c-b^2c+c\)
\(=\left(ab^2c^2+ba^2c^2+ca^2b^2\right)+\left(a+b+c\right)\)
\(-\left(ab^2+ac^2+a^2b+bc^2+a^2c+b^2c\right)\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)\)\(-\left[ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\right]\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)+3abc\)\(-\left[ab\left(a+b+c\right)+bc\left(a+b+c\right)+ca\left(a+b+c\right)\right]\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)+3abc\)\(-\left(a+b+c\right)\left(ab+bc+ca\right)\)
\(=abc\left(bc+ac+ab\right)+abc+3abc\)\(-abc\left(ab+bc+ca\right)=4abc\)
Vậy \(a\left(b^2-1\right)\left(c^2-1\right)+b\left(a^2-1\right)\left(c^2-1\right)+c\left(a^2-1\right)\left(b^2-1\right)=4abc\)(đpcm)

Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
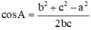
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.


áp dụng BDT AM-GM
\(=>a^2+b^2+c^2\ge3\sqrt[3]{\left(abc\right)^2}\)
\(=>1\ge3\sqrt[3]{\left(abc\right)^2}=>1\ge27\left(abc\right)^2\)\(=>27\left(abc\right)^2\le1=>3\left(abc\right)^2\le\dfrac{1}{9}=>\left(abc\right)^2\le\dfrac{1}{27}=>abc\le\dfrac{1}{3\sqrt{3}}\)
\(=>\dfrac{8}{9abc}\ge\dfrac{8}{9.\dfrac{1}{3\sqrt{3}}}=\dfrac{8\sqrt{3}}{3}\)
\(S=a+b+c+\dfrac{1}{abc}=a+b+c+\dfrac{1}{9abc}+\dfrac{8}{9abc}\)
\(=>a+b+c+\dfrac{1}{9abc}\ge4\sqrt[4]{\dfrac{1}{9}}=\dfrac{4}{\sqrt{3}}\)
\(=>S\ge\dfrac{4}{\sqrt{3}}+\dfrac{8}{\sqrt{3}}=4\sqrt{3}\)
dấu"=" xyar ra<=>a=b=c=\(\dfrac{1}{\sqrt{3}}\)
Các bn mà cop thì nhớ giải thích giúp mik đoạn \(a^2+b^2+c^2\ge3\sqrt[3]{abc}\) với

Với số tự nhiên a bất kì thì a^2 chia 3 dư 0,1 ( Xét a=3k,a=3k+1,a=3k+2 )
Áp dụng :
VT chia 3 dư 0,1,2 VP chia 3 dư 0,1.
Do đó muốn có nghiệm thì a,b không được cùng số dư là 1 khi chia cho 3
=>Tồn tại một số chia hết cho 3.
Tương tự: a^2 chia 4 dư 0,1(xét a=4k,a=4k+1,a=4k+2,a=4k+3)
=>Tồn tại một số chia hết cho 4
a^2 chia 5 dư 0,1,4(xét a=5k,...)
VT chia 5 dư 0,1,2,3,4 mà VP chia 5 dư 0,1,4
Xảy ra khi tồn tại ít nhất một số bên vế phải chia hết cho 5
=>abc chia hết cho 3x4x5=60 (đpcm)
Giả thiết a, b, c nguyên; a² = b²+c²
* ta biết số chính phương: n² khi chia 3 dư 0 hoặc dư 1
từ a² = b²+c², thấy b² và c² khi chia 3 không thể cùng dư 1
vì nếu chúng cùng dư 1 thì a² = b²+c² chia 3 dư 2 vô lí
=> hoặc b², hoặc c² có ít nhất 1 số chia 3 dư 0 => b hoặc c chia hết cho 3
=> abc chia hết cho 3 (1)
* ta biết số n² chia 4 dư 0 hoặc dư 1
nếu n chẳn => n² chia 4 dư 0
nếu n lẻ: n = 2k+1 => (2k+1)² = 4k²+4k+1 chia 4 dư 1
từ a² = b²+c² => b² và c² khi chia 4 không thể cùng dư 1
vì nếu b² và c² chia 4 đều dư 1 => b²+c² = a² chia 4 dư 2 trái lí luận trên
=> hoặc b² hoặc c² (hoặc cả 2) chia 4 dư 0, chẳn hạn b² chia 4 dư 0
+ nếu c² chia 4 dư 0 => b và c đều chia hết cho 2 => abc chia hết cho 4
+ nếu c² chia 4 dư 1 => a² = b²+c² chia 4 dư 1 => a, c là 2 số lẻ
a = 2n+1 ; c = 2m+1; có: b² = a²-c² = (a-c)(a+c) = (2n-2m)(2n+2m+2)
=> b² = 4(n-m)(n+m+1) (**)
ta lại thấy nếu m, n cùng chẳn hoặc cùng lẻ => n-m chẳn
nếu m, n có 1 chẳn, 1 lẻ => m+n+1 chẳn
=> (m-n)(m+n+1) chia hết cho 2 => b² = 4(m-n)(m+n+1) chia hết cho 8
=> b chia hết cho 4 => abc chia hết cho 4
Tóm lại abc luôn chia hết cho 4 (2)
* lập luận tương tự thì thấy số n² chia cho 5 chỉ có thể dư 0, 1, 4
+ b² và c² chia 5 không thể cùng dư 1 hoặc 4
vì nếu cùng dư 1 => b²+c² = a² chia 5 dư 2
nếu cùng dư là 4 thì b²+c² = a² chia 5 dư 3
đều vô lí do a² chia 5 chỉ có thể dư 0, 1 hoặc 4
+ b² chia 5 dư 1 và c² chia 5 dư 4 (hoặc ngược lại)
=> b²+c² = a² chia 5 dư 0 => a chia hết cho 5 (do 5 nguyên tố)
+ nếu b² hoặc c² chia 5 dư 0 => b (hoặc c ) chia hết cho 5
Tóm lại vẫn có abc chia hết cho 5 (3)
Từ (1), (2), (3) => abc chia hết cho 3, 4, 5
=> abc chia hết cho [3,4,5] = 60