Một hỗn hợp gồm 2 đồng vị có số khối trung bình là 31,1 và tỷ lệ phần trăm của các đồng vị là 90% và 10%. Tổng số hạt cơ bản trong 2 đồng vị là 93. Số hạt không mang điện bằng 0,55 lần số hạt mang điện. Tìm số điện tích hạt nhân và số nơtron trong mỗi đồng vị?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LM
Lương Minh Hằng
24 tháng 6 2019
Đúng(0)
Những câu hỏi liên quan
3 tháng 8 2017
Đáp án B
Gọi Z ; N 1 ; N 2 lần lượt là số proton và nơtron của 2 đồng vị đã cho
0 , 9 ( Z + N 1 ) + 0 , 1 ( Z + N 2 ) = 31 , 1 4 Z + ( N 1 + N 2 ) = 93 N 1 + N 2 = 0 , 55 . 4 Z ⇔ Z = 15 N 1 = 16 N 2 = 17
24 tháng 4 2019
Gọi Z ; N 1 ; N 2 lần lượt là số proton và nơtron của 2 đồng vị đã cho
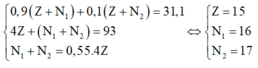
Đáp án B
QD
8 tháng 10 2021
Đặt đồng vị thứ nhất là ZA1X có số nơtron là N1, đồng vị thứ 2 là ZA2X có số nơtron là N2 (vì 2 đồng vị thuộc cùng 1 nguyên tố nên Z và E như nhau)
+) Số khối trung bình: ¯A=90.A1+10.A2100=0,9.A1+0,1.A2=31,1A¯=90.A1+10.A2100=0,9.A1+0,1.A2=31,1
Vì A = Z + N => 0,9.(Z + N1) + 0,1.(Z + N2) = 31,1
=> 100Z + 90N1 + 10N2 = 3110 (1)
+) Tổng số các hạt trong 2 đồng vị là 93:
=> E + Z + N1 + E + Z + N2 = 93
=> (2Z + N1) + (2Z + N2) = 93 => 4Z + N1 + N2 = 93 (2)
+) Tổng số hạt không mang điện bằng 0,55 lần tổng số hạt mang điện
=> N1 + N2 = 0,55.(Z + E + Z + E)
=> N1 + N2 = 0,55.4Z = 2,2Z (3)
Từ (1), (2) và (3) => Z = 15; N1 = 16; N2 = 17
N
3 tháng 8 2019
Tổng hạt trong đồng vị 1 = 2Z + N1
Tổng hạt trong đồng vị 2 = 2Z + N2
—> 4Z + N1 + N2 = 93 và 4Z.0,55 = N1 + N2
—> Z = 15 và N1 + N2 = 33 (1)
—> [90(N1 + 15) + 10(N2 + 15)]/100 = 31,1 (2) (1)(2)
—> N1 = 16 và N2 = 17
KH
3 tháng 8 2019
Theo đề bài ta có:
\(\\ ĐV_1=A_1;ĐV_2=A_2\\ hpt:\left\{{}\begin{matrix}2p+n_1+2p+n_2=93\\n_1+n_2=0,55\left(2p+2p\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=15\\n_1+n_2=33\left(1\right)\end{matrix}\right.\)
\(\frac{x\%.A_1+y\%.A_2}{100}=31,1\Leftrightarrow\frac{90\left(p+n_1\right)+10\left(p+n_2\right)}{100}=31,1\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}n_1=16\\n_2=17\end{matrix}\right.\)
13 tháng 1 2022
Có
+) 2pY + nY = 43
+) \(2p_Y=\dfrac{28}{15}n_Y\)
=> \(\left\{{}\begin{matrix}p_Y=14\\n_Y=15\end{matrix}\right.\) => AY = 14 + 15 = 29 => AX = 28
=> \(\overline{M}=\dfrac{28.90+29\left(100-90\right)}{100}=28,1\)
16 tháng 6 2018
Đáp án C
Đồng vị X1 có tổng số hạt là 18 → 2Z1 + N1 = 18
Trong X1 có các loại hạt bằng nhau
→ Z1= N1 =
18
3
= 6 → A1 = Z1 + N1 = 12
Đồng vị X2 có tổng số hạt là 20
→ 2Z2 + N2 = 20
Luôn có Z2=Z1 ( cùng là đồng vị của nguyên tố X)
→ Z2 = 6 → N2 = 8 → A2 = 6 + 8 = 14
Nguyên tử khối trung bình của X là
M X = ( 50 . 12 + 20 . 14 ) / 100 = 13
14 tháng 7 2018
Đáp án C
Các loại hạt trong X1 bằng nhau → pX1 = nX1 = 18 : 6
Vì X1 và X2 là đồng vị → pX1 =pX2 =6
Tổng số hạt trong X2 là 20 → 2pX2 + nX2 = 20 → nX2 = 8
Số khối của X1 là 12, số khối của X2 là 14
Nguyên tử khối trung bình của X là 50 . 12 + 50 . 14 100 . 100 = 13