Cho tam giác ABC , đường trung tuyến AM , BN , CP . Chứng minh BN +CP > 3/2 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1
T
24 tháng 6 2019
A B C M N P G
Gọi giao điểm của ba đường trung tuyến AM, BN, CP là G (G là trọng tâm)
Theo tính chất trọng tâm. Ta có: \(BG+CG=\frac{2}{3}\left(BN+CP\right)\) (1)
Mặt khác theo BĐT tam giác: \(BG+CG>BC\) (2)
Từ (1) và (2) suy ra \(\frac{2}{3}\left(BN+CP\right)>BC\). Nhân \(\frac{3}{2}\) vào hai vế của BĐT ta được:
\(BN+CP>\frac{3}{2}BC\) (đpcm)
17 tháng 9 2023
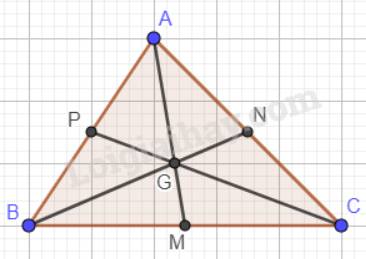
Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\)độ dài đường trung tuyến đi qua đỉnh ấy nên:
\(\begin{array}{l}\dfrac{{GA}}{{AM}} = \dfrac{{GB}}{{BN}} = \dfrac{{GC}}{{CP}} = \dfrac{2}{3}\\ \to GA = \dfrac{2}{3}AM;GB = \dfrac{2}{3}BN;GC = \dfrac{2}{3}CP\end{array}\)
Vậy:
\(GA + GB + GC = \dfrac{2}{3}AM + \dfrac{2}{3}BN + \dfrac{2}{3}CP = \dfrac{2}{3}(AM + BN + CP)\).
NT
0
30 tháng 1 2016
các trường hợp đồng dạng của tam giác thường :
Trường hợp đồng dạng 1 : 3 cạnh tương ứng tỉ lệ với nhau (c – c – c)
xét ∆ABC và ∆DEF, ta có :
=> ∆ABC ~ ∆DEF (c – c – c)
Trường hợp đồng dạng 2 : 2 cạnh tương ứng tỉ lệ với nhau – góc xen giữa hai cạnh bằng nhau(c – g – c)
xét ∆ABC và ∆DEF, ta có :
=> ∆ABC ~ ∆DEF (c – g – c)
Trường hợp đồng dạng 3 : hai góc tương ứng bằng nhau(g – g)
xét ∆ABC và ∆DEF, ta có :
=> ∆ABC ~ ∆DEF (g – g)
A b C B M N P G
Gọi G là trọng tâm tam giác ABC
Vì là trung tuyến \(\Rightarrow\hept{\begin{cases}BN=\frac{3}{2}BG\\CP=\frac{3}{2}CG\end{cases}}\)
\(\Rightarrow BN+CP=\frac{3}{2}\left(BG+CG\right)\)
Mà theo bđt trong tam giác cho tam giác BGC thì \(BG+GC>BC\)
\(\Rightarrow BN+CP>\frac{3}{2}BC\)