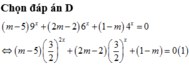Có bao nhiêu giá trị nguyên của m để bất phương trình \(5mx\le2x+2m^2-m+2\) nhận nghiệm nguyên lớn nhất bằng 1?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VN
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 6 2019
\(\Leftrightarrow\left(5m-2\right)x\le2m^2-m+2\)
- Với \(m=\frac{2}{5}\Rightarrow BPT\) đúng với mọi x \(\Rightarrow\) loại
- Với \(m< \frac{2}{5}\Rightarrow x\ge\frac{2m^2-m+2}{5m-2}\) \(\Rightarrow\) không tồn tại GTLN của x (loại)
- Với \(m>\frac{2}{5}\Rightarrow x\le\frac{2m^2-m+2}{5m-2}\)
Để BPT nhận nghiệm nguyên lớn nhất bằng 1
\(\Rightarrow\frac{2m^2-m+2}{5m-2}< 2\)
\(\Leftrightarrow2m^2-m+2< 10m-4\)
\(\Leftrightarrow2m^2-11m+6< 0\)
\(\Rightarrow\frac{11-\sqrt{73}}{4}< m< \frac{11+\sqrt{73}}{4}\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)
28 tháng 7 2021
\(mx^2-2\left(m+2\right)x+2m-1< 0\)
\(< =>mx^2-2\left(m+2\right)x+2m-1\ge0\)
\(a=m\ne0\)
\(\Delta=\left(2m+2\right)^2-4m\left(2m-1\right)\)
\(\Delta=4m^2+8m+4-8m^2+4m\)
\(\Delta=12m-4m^2+4\)
\(< =>\hept{\begin{cases}a>0\\\Delta\le0\end{cases}\hept{\begin{cases}m>0\\12m-4m^2+4\le0\end{cases}\hept{\begin{cases}m>0\\m=\left[\frac{3-\sqrt{13}}{2};\frac{3+\sqrt{13}}{2}\right]\end{cases}}}}\)
\(< =>m=(0;\frac{3+\sqrt{13}}{2}]\)
vậy m vô số nghiệm để bpt vô nghiệm
CM
17 tháng 12 2019
Đáp án D.
Ta có:
P T ⇔ m 9 4 x − 2 m + 1 6 4 x + m ≤ 0 ⇔ m 3 2 2 x − 2 m + 1 3 2 x + m ≤ 0
Đặt t = 3 2 x ; do x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 . Khi đó PT trở thành: m t 2 − 2 m + 1 t + m ≤ 0 ⇔ m t 2 − 2 t + 1 ≤ t
Rõ ràng t = 1 là nghiệm của BPT đã cho.
Với t ∈ 1 ; 3 2 ⇒ m ≤ t t − 1 2 = f t , xét f x với t ∈ 1 ; 3 2 ta có:
f ' t = t − 1 − 2 t t − 1 3 = − t − 1 t − 1 2 < 0 ∀ t ∈ 1 ; 3 2
do đó f t nghịch biến trên 1 ; 2 3 .
Do đó BPT nghiệm đúng vơi ∀ t ∈ 1 ; 3 2 ⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6
Vậy có 6 giá trị nguyên dương của m thỏa mãn.
CM
1 tháng 4 2017
Đáp án D.
Ta có:
P T ⇔ m 9 4 x - 2 m + 1 6 4 x + m ≤ 0
⇔ m 3 2 2 x - 2 m + 1 3 2 x + m ≤ 0
Đ ặ t t = 3 2 x ; d o x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 .
Khi đó PT trở thành:
m t 2 - 2 m + 1 t + m ≤ 0 ⇔ m t 2 - 2 t + 1 ≤ t
Rõ ràng t =1 là nghiệm của BPT đã cho.
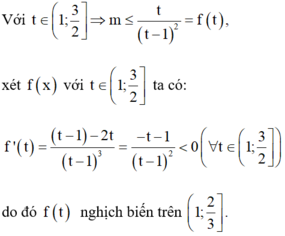
D o đ ó B P T n g h i ệ m đ ú n g v ớ i ∀ t ∈ 1 ; 3 2
⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6 .
Vậy có 6 giá trị nguyên dương của m thỏa mãn.
CM
3 tháng 11 2018
Chọn B.
Đặt t= 5x> 0.
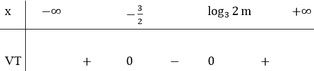
+ Phương trình đã cho trở thành: t2-( m+2) t+2m-1=0 suy ra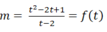 
( 2)
( với t= 2 phương trình vô nghiệm).
Do đó phương trình đã cho có nghiệm khi phương trình (2) có nghiệm t> 0 .
+ Lập bảng biến thiên của hàm số f(t) dựa vào bảng biến thiên suy ra m ≤ 0 m ≥ 4
kết hợp điều kiện m nguyên và m ∈ [0;2018] => m ∈ {0;4;5;6;...;2018}
Vậy nghiệm 2016 giá trị của m thỏa mãn yêu cầu bài toán ra
