Hãy xác định tâm và bán kính đường tròn ngoại tiếp của các hình sau:
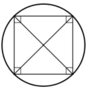
1, Hình vuông 3, hình thang cân
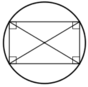
2, HCN. 4, hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các hình nội tiếp được trong một đường tròn là:
+ Hình chữ nhật:
Hình chữ nhật ABCD có:
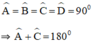
⇒ ABCD nội tiếp trong một đường tròn. Đường tròn đó là đường tròn đường kính AC.
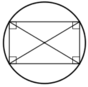
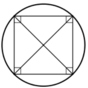
+ Hình vuông:
Vì hình vuông là hình chữ nhật
⇒ Hình vuông cũng nội tiếp trong một đường tròn.
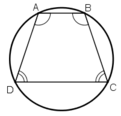
+ Hình thang cân:
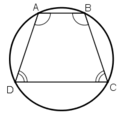
Hình thang cân ABCD có:
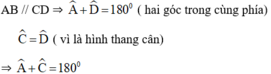
⇒ ABCD nội tiếp trong một đường tròn.

Các hình nội tiếp được trong một đường tròn là:
+ Hình chữ nhật:
Hình chữ nhật ABCD có:
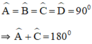
⇒ ABCD nội tiếp trong một đường tròn. Đường tròn đó là đường tròn đường kính AC.
+ Hình vuông:
Vì hình vuông là hình chữ nhật
⇒ Hình vuông cũng nội tiếp trong một đường tròn.
+ Hình thang cân:
Hình thang cân ABCD có:
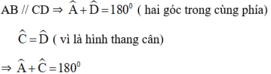
⇒ ABCD nội tiếp trong một đường tròn.

Gọi O là trung điểm AD
\(\Rightarrow OA=OB=OC=OD=a\)
\(\Rightarrow\) O là tâm đường tròn ngoại tiếp đáy
Gọi I là trung điểm SD \(\Rightarrow IO\perp\left(ABCD\right)\) đồng thời I là tâm đường tròn ngoại tiếp SAD (tam giác SAD vuông tạm A)
\(\Rightarrow I\) là tâm mặt cầu ngoại tiếp
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{2}\)
\(\Rightarrow R=\dfrac{1}{2}SD=a\sqrt{2}\)

Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng 180o.Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là 90o + 90o = 180o
Hình thang nói chung, hình thang vuông không nội tiếp được đường tròn.
Hình thang cân ABCD (BC= AD) có hai góc ở mỗi đáy bằng nhau
=
,
=
; mà
+
= 180o (hai góc trong cùng phía tạo bởi cát tuyến AD với AD // CD),suy ra
+
= 180o . Vậy hình thang cân luôn có tổng hai góc đối diện bằng 180o nên nội tiếp được đường tròn

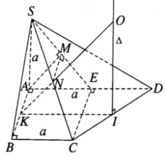
Tam giác CED là tam giác vuông cân tại E nên trục của đường tròn đi qua ba điểm C, E, D là đường thẳng ∆ đi qua trung điểm I của đoạn thẳng CD và song song với SA.
Gọi M, N lần lượt là trung điểm của SE và SC. Ta có mặt phẳng (ABNM) là mặt phẳng trung trực của đoạn SE. Vậy tâm O của mặt cầu ngoại tiếp hình chóp S.CDE chính là giao điểm của Δ và mp(ABNM). Gọi K là trung điểm của AB thì KN // AM và do đó KN //(SAE). Ta có IK // AD nên IK // (SAE).
Vậy KN và ∆ đồng phẳng và ta có O là giao điểm cần tìm.
Chú ý rằng OIK là tam giác vuông cân, vì ∠ OKI = ∠ MAE = 45 °
Ta có OI = IK, trong đó
![]()
Vậy
![]()
![]()
Do đó, bán kính mặt cầu ngoại tiếp hình chóp S.CDE là:
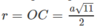
1) tâm : giao điểm của 2 đường chéo bán kính \(\frac{r}{\sqrt{2}}\)( với r là cạnh hình vuông )
2) tâm : giao điểm của 2 đường chéo bán kính \(\frac{1}{2}\sqrt{a^2+b^2}\)( với a,b là các cạnh của hình vuông)
3) tâm : giao điểm của 2 đường chéo
4) không có tâm