Bài 1: Tính
a) \(\sqrt{125}-4\sqrt{45}+3\sqrt{20}-\sqrt{80}\)
b) \(\sqrt{29^2-20^2}\)
c) \(3\sqrt{2}\left(\sqrt{50}-2\sqrt{18}+\sqrt{98}\right)\)
d) \(\sqrt{4-\sqrt{15}}-\sqrt{4+\sqrt{15}}\)
e) \(\sqrt{3-\sqrt{5}}\left(3+\sqrt{5}\right)\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
f) \(2\sqrt{5}-\sqrt{125}-\sqrt{80}+\sqrt{605}\)
g) \(\sqrt{3}-3\sqrt{12}+4\sqrt{27}+3\)
Bài 2: Tìm ĐKXĐ
1) \(\sqrt{-x^2-5}\)
2) \(\frac{\sqrt{x-4}}{3}\)
3) \(\sqrt{\frac{-3}{x+1}}\)
4) \(\sqrt{\frac{-x^2-1}{x-3}}\)


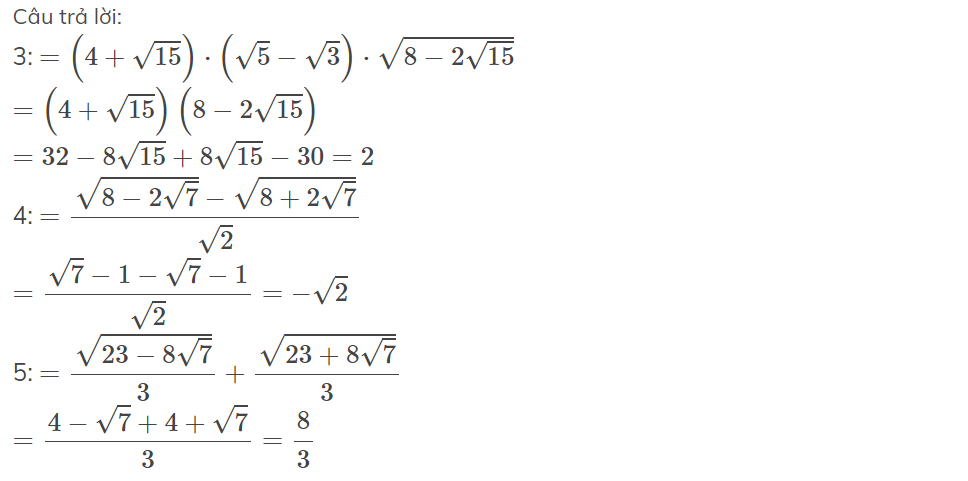
a/ \(=5\sqrt{5}-12\sqrt{5}+6\sqrt{5}-4\sqrt{5}=-5\sqrt{5}\)
Mấy câu kia bấm máy tính là xong hết
B2:
a/ \(=\sqrt{-\left(x^2+5\right)}\)
Có \(x^2+5>0\forall x\Rightarrow-\left(x^2+5\right)< 0\forall x\)
Vậy biểu thức luôn ko đc xđ
b/ x-4\(\ge0\) \(\Rightarrow x\ge4\)
c/ Có -3<0
Để căn thức xđ\(\Leftrightarrow x+1< 0\Leftrightarrow x< -1\)
d/ Có -(x2+1)<0\(\forall\) x
Để căn thức có nghĩa \(\Leftrightarrow x-3< 0\Leftrightarrow x< 3\)