Tìm tất cả giá trị của m để phương trình mx-√x−3= m+1 có 2 nghiệm thực phân thực biệt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
.
.
.
.
CM
6 tháng 9 2018
Đáp án C
Điều kiện của phương trình 
là 
hay 
Với điều kiện đó 
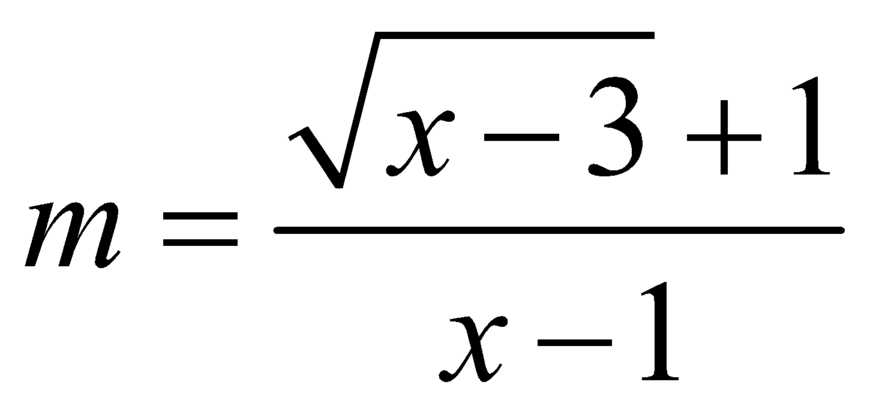
Xét hàm số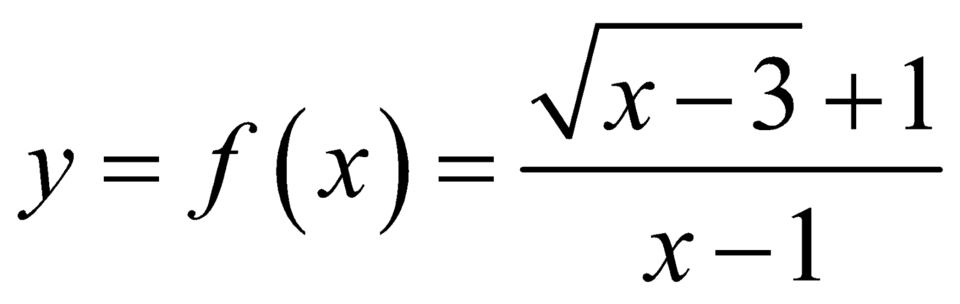 
với 
.
Trên 
, ta có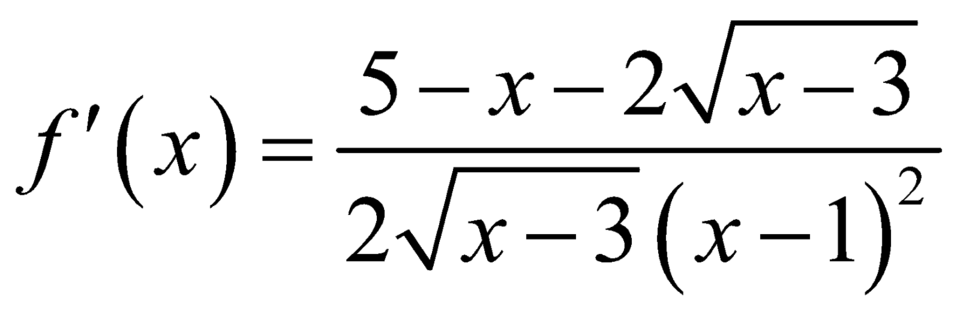 
,
.
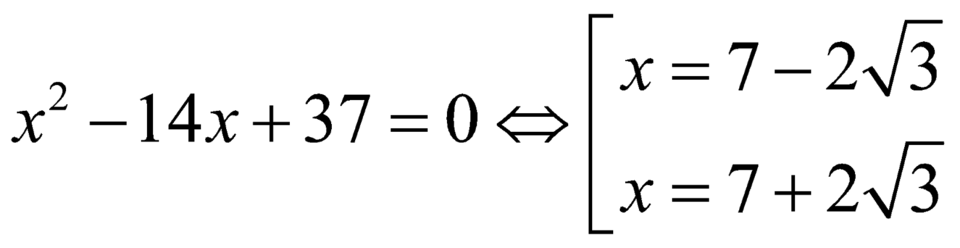Chỉ có giá trị 
thỏa.
Vẽ đồ thị, ta thấy với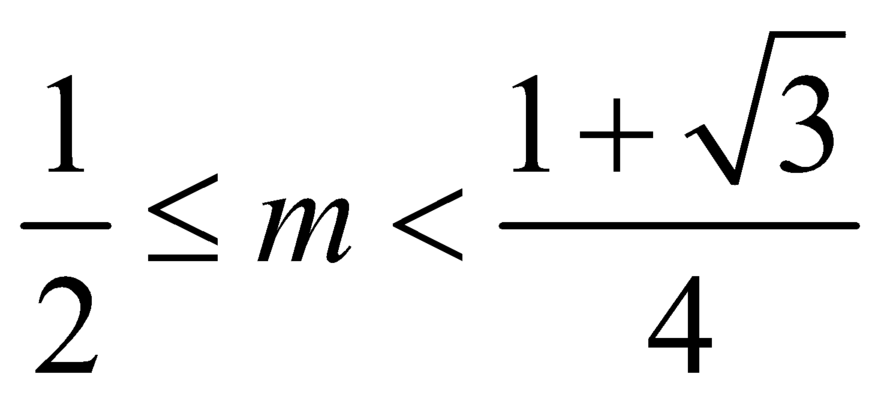 
thì đường thẳng y=m cắt đồ thị hàm số 
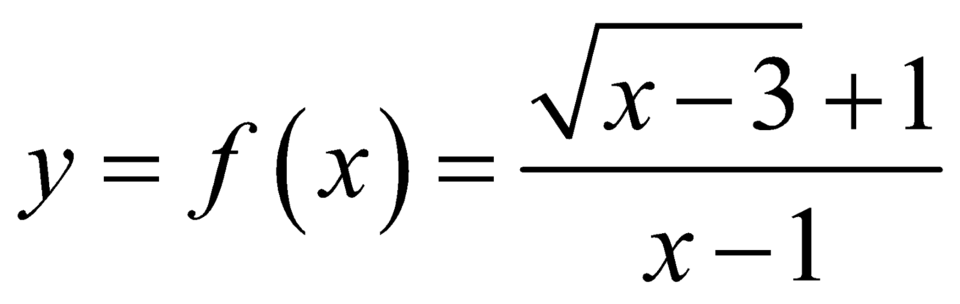tại hai điểm phân biệt.
Vậy phương trình 
có hai nghiệm phân biệt khi và chỉ khi 
.
GB
1
RH
4 tháng 2 2024
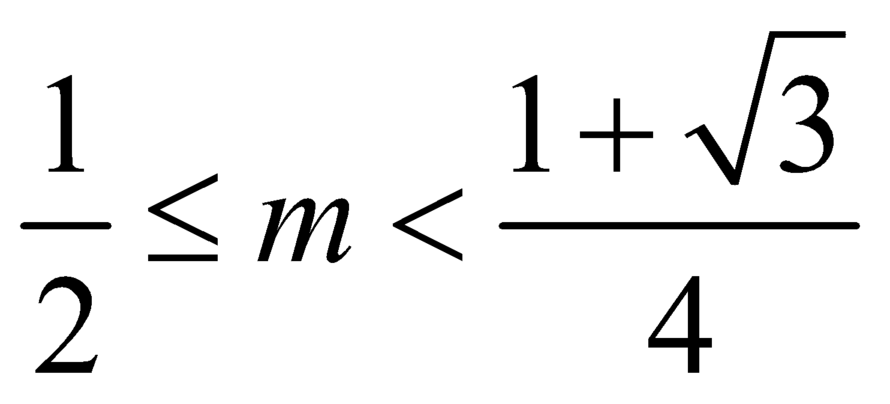Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-2t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt dương: \(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1-m>0\\2>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)
ND
1
24 tháng 11 2021
\(x-4\sqrt{x+3}+m=0\)
\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)
\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)
\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)
\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)
\(\Rightarrow f\left(0\right)=-3\)
\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
15 tháng 12 2021
\(t^2-4t-3+m=0\Leftrightarrow t^2-4t-3=-m\)
\(có-2nghiệm-pb-trên[0;\text{+∞})\)
\(xét-bảng-biến-thiên-củaf\left(t\right)=t^2-4t-3,trên[0;\text{+∞})\)
f(t) 0 2 +∞ -∞ -3 -7 -m -m t
dựa vào bảng biến thiên ta thấy số nghiệm của phương trình f(t)
là số giao điểm của đường thẳng y=-m
\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)
CM
27 tháng 8 2017
Đáp án C
Ta có: x . log 2 x − 1 + m = m . log 2 x − 1 + x
⇔ x − m . log 2 x − 1 = x − m .
⇔ x − m log 2 x − 1 − 1 ⇔ x − m = 0 log 2 x − 1 = 1 ⇔ x = m x − 1 = 2 ⇔ x = m x = 3 *
Để phương trình đã cho có 2 nghiệm phân biệt ⇔ * có nghiệm duy nhất x > 1 ; x ≠ 3. Vậy m > 1 v à m ≠ 3 là giá trị cần tìm.
CM
12 tháng 6 2018
Đáp án D
Phương trình x + 1 = m 2 x 2 + 1 ⇔ m = x + 1 2 x 2 + 1 ; ∀ x ∈ ℝ
Xét hàm số f x = x + 1 2 x 2 + 1 trên ℝ có f ' x = 1 - 2 x 2 x 2 + 1 3 = 0 ⇔ x = 1 2 .
Tính các giá trị f 1 2 = 6 2 ; lim x → + ∞ f x = 1 2 ; lim x → - ∞ f x = - 1 2
Khi đó, để f(x) = m có 2 nghiệm phân biệt ⇔ 2 2 < m < 6 6 .
CM
8 tháng 9 2019
Chọn D
Điều kiện x ≥ 1
Ta có phương trình 3 x - 1 + m x + 1 = 2 x 2 - 1 4
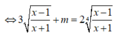
Đặt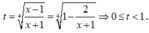 
Phương trình trở thành: 
Nhận xét: Mỗi giá trị của t ∈ [0;1) cho ta 1 nghiệm x ∈ [1;+ ∞ )
Do đó phương trình đã cho có 2 nghiệm thực phân biệt
⇔ phương trình (1) có nghiệm phân biệt t ∈ [0;1)
Bảng biến thiên:
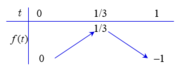
Từ bảng biến thiên suy ra 0 ≤ m < 1 3
ĐKXĐ: \(x\ge3\)
\(\Leftrightarrow mx-\sqrt{x-3}=m+1\Leftrightarrow m\left(x-1\right)=\sqrt{x-3}+1\)
\(\Leftrightarrow m=\frac{\sqrt{x-3}+1}{x-1}\)
Đặt \(\sqrt{x-3}=t\ge0\) \(\Rightarrow x=t^2+3\Rightarrow m=\frac{t+1}{t^2+2}\)
Xét hàm \(f\left(t\right)=\frac{t+1}{t^2+2}\Rightarrow f'\left(t\right)=\frac{t^2+2-2t\left(t+1\right)}{\left(t^2+2\right)^2}=\frac{-t^2-2t+2}{\left(t^2+2\right)^2}\)
\(f'\left(t\right)=0\Rightarrow t=\sqrt{3}-1\)
Ta có \(f\left(\sqrt{3}-1\right)=\frac{1+\sqrt{3}}{4}\); \(\lim\limits_{t\rightarrow+\infty}\frac{t+1}{t^2+1}=0\); \(f\left(0\right)=\frac{1}{2}\)
Dựa vào BBT, để pt đã cho có 2 nghiệm pb thì \(\frac{1}{2}\le m< \frac{1+\sqrt{3}}{4}\)