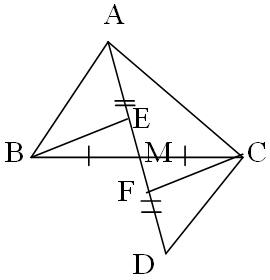
Cho tam giác ABC vuông tại A, trung tuyến AM. Trên tia đối MA lấy D sao cho DM = MA
1. Chứng minh : Tam giác ABC = tam giác DCM và DC vuông góc với AC
2. Trên tia đối AB láy E sao cho EA = AB . EM cắt AC tại N . Chứng minh NC = 2NA
3. Chứng minh : \(\frac{AB+AC-BC}{2}< AM< \frac{AB+AC}{2}\)



( Thông cảm hình bị lệch )
a) + Xét \(\Delta ABC\)và \(\Delta DMC\)có :
AM = DM ( gt )
\(\widehat{AMB}=\widehat{DMC}\)( vì là hai góc đối đỉnh ) => \(\Delta AMB=\Delta DMC\)
MB = MC ( AM là trung tuyến của \(\Delta ABC\))
=> \(\widehat{B}=\widehat{MCD}\)( hai góc tương ứng )
=> DC // AB ( có hai góc so le trong = )
Mà AB \(\perp\)AC ( Vì \(\Delta ABC\)vuông tại A)
=> DC _|_ AC
+ Xét \(\Delta BEC\)có :
M là trung điểm của cạnh BC ( Vì AM là trung tuyến của ABC )
=> EM là trung tuyến
A là trung điểm của BE ( Vì EA = AB ) => CA là trung tuyến
Mà EM cắt AC tại N => N là trọng tâm của \(\Delta ABC\)
\(\Rightarrow NC=\frac{2}{3}CA\Rightarrow NC=2NA\)
+ Ta có \(\Delta AMB=\Delta DMC\Rightarrow AB=CD\)
Xét \(\Delta ACD\)có :
CD + AC > AD ( bđt tam giác ) . Mà CD = AB ; AD = 2AM
=> \(AB+AC>2AM\Leftrightarrow\frac{AB+AC}{2}>AM\)(1)
+ Xét \(\Delta AMB\)có : AM > AB - BM
\(\Delta AMC\)có : AM > AC - CM
=> 2AM > AB + AC - BM - CM
<=> 2AM > AB + AC - (BM +CM )
<=> 2AM > AB + AC - BC
<=> AM > \(\frac{AB+AC-BC}{2}\)(2)
Từ (1), (2) => Điều cần cm trên đề bài .