Cho khối chóp ABCDA’B’C’D’ cạnh a . Gọi S là điểm thuộc đường thẳng AA’ sao cho A’ là trung điểm của SA. Tính thể tích phần khối chóp SABD nằm trong khối lập phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 5 2019
Nối \(SB';SC';SD'\) lần lượt cắt \(A'B';A'C';A'D'\) tại M, N, P
\(\Rightarrow M,N,P\) là trung điểm của A'B', A'C', A'D' theo tính chất đường trung bình
\(\Rightarrow A'MNP\) là hình vuông cạnh \(\frac{a}{2}\)
\(V_{A'MNP.ABCD}=V_{S.ABCD}-V_{S.A'MNP}=\frac{1}{3}\left(SA.AB^2-SA'.AM^2\right)\)
\(=\frac{1}{3}\left(2a.a^2-a.\left(\frac{a}{2}\right)^2\right)=\frac{7a^3}{12}\)

CM
12 tháng 11 2017
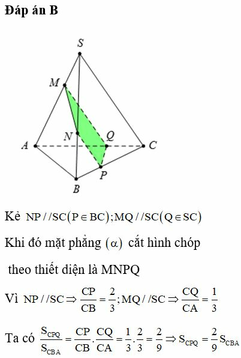
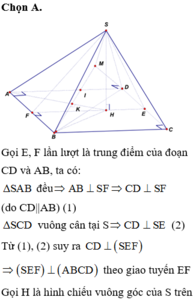
Chọn B
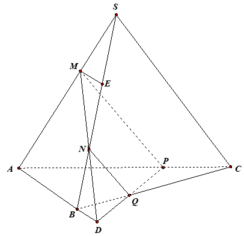
Trong mặt phẳng (SAC) dựng MP song song với SC cắt AC tại P. Trong mặt phẳng (SBC) dựng NQ song song với SC cắt BC tại Q. Gọi D là giao điểm của MN và PQ. Dựng ME song song với AB cắt SB tại E (như hình vẽ).
Ta thấy: ![]()
Suy ra N là trung điểm của BE và DM, đồng thời
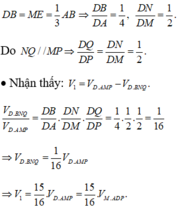
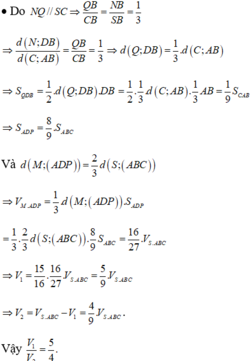
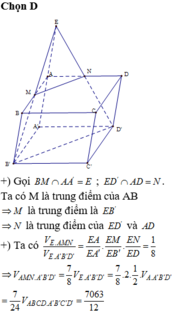
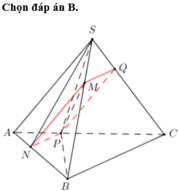
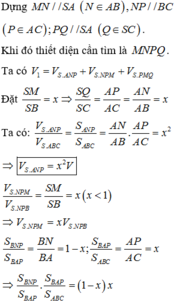
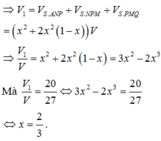
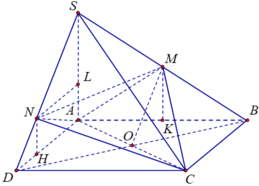
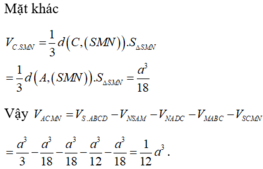

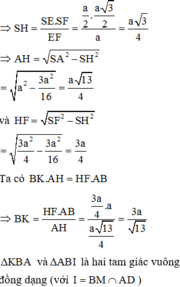

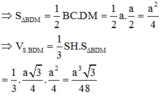
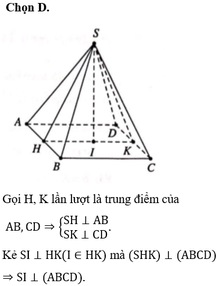

Gọi giao của SB với \(A'B'\) là M, giao của \(SD\) với \(A'D'\) là N
\(\Rightarrow M,N\) lần lượt là trung điểm A'B' và A'D'
\(\Rightarrow\Delta MA'N\) vuông cân tại A' với \(A'M=A'N=\frac{a}{2}\)
\(V_{A'MN.ABD}=V_{S.ABD}-V_{SA'MN}=\frac{1}{6}\left(SA.AB^2-SA'.A'M^2\right)\)
\(=\frac{1}{6}\left(2a.a^2-a.\left(\frac{a}{2}\right)^2\right)=\frac{7a^3}{24}\)