Question

[Mai Thảo]

Giải giúp em vài bài toán chuyên đề lượng giác 11 với ạ!!

1) Tìm GTLN, GTNN của y=\(\sqrt{sinx}-\sqrt{cosx}\)

2) Tìm tập giá trị của hàm số y= tan2x + cot2x

3) Tìm tập hợp T các giá trị thực cùa tham số m để hàm số y= mtanx +2 tăng trong khoảng (0;\(\frac{\Pi}{2}\))

4) Tìm tập giá trị của hàm số y=\(|tanx+cotx|\)

5) Một chất điểm dao động điều hòa quanh vị trí cân bằng với phương trình dao động được cho bởi x=100sin(\(\frac{\Pi}{3}t\))cm, trong đó thời gian t tính bằng giây. Ở giây thứ 5 kể từ lúc bắt đầu dao động, chất điểm cách vị trí cân bằng bao nhiêu?

6) Một đường đua ô tô dạng đường tròn có bán kính 1km. Trên đường đua người ta đặt 3 trạm tiếp nhiên liệu cách đều nhau. Khoảng cách giữa các trạm tiếp nhiên liệu là bao nhiêu (kết quả làm tròn đến hàng phần nghìn)?

Answer 1

[Nguyễn Việt Lâm]

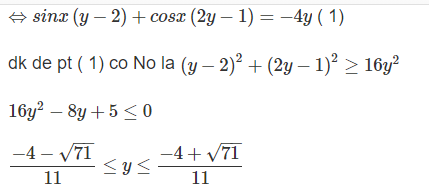
Câu 1:

\(\left\{{}\begin{matrix}\sqrt{sinx}\le1\\\sqrt{cosx}\ge0\end{matrix}\right.\) \(\Rightarrow y=\sqrt{sinx}-\sqrt{cosx}\le1-0=1\)

\(\Rightarrow y_{max}=1\) khi \(x=\frac{\pi}{2}+k2\pi\)

\(\left\{{}\begin{matrix}\sqrt{sinx}\ge0\\\sqrt{cosx}\le1\end{matrix}\right.\) \(\Rightarrow y=\sqrt{sinx}-\sqrt{cosx}\ge0-1=-1\)

\(\Rightarrow y_{min}=-1\) khi \(x=k2\pi\)

Câu 2:

- Nếu \(tan2x>0\Rightarrow cot2x>0\Rightarrow y\ge2\sqrt{tan2x.cot2x}=2\)

- Nếu \(tan2x< 0\Rightarrow cot2x< 0\Rightarrow y=-\left(\left|tan2x\right|+\left|cot2x\right|\right)\le-2\sqrt{\left|tan2x\right|.\left|cot2x\right|}=-2\)

\(\Rightarrow\left\{{}\begin{matrix}y\ge2\\y\le-2\end{matrix}\right.\)

Câu 3:

Do \(tanx\) là hàm tăng nên để \(y=mtanx+2\) là hàm tăng thì \(m>0\)

Answer 2

[Nguyễn Việt Lâm]

Câu 4:

Ta thấy \(y\ge0\)

\(y^2=\left(tanx+cotx\right)^2=tan^2x+cot^2x+2\ge2tanx.cotx+2=4\)

\(\Rightarrow\left|y\right|\ge2\)

Mà \(y\ge0\Rightarrow y\ge2\)

Câu 5:

Tọa độ của chất điểm ở giây thứ 5:

\(x=100sin\left(\frac{5\pi}{3}\right)=-50\sqrt{3}\) (cm)

Vậy chất điểm nằm cách vị trí cân bằng \(50\sqrt{3}\) (cm) về phía chiều âm

Câu 6:

Chu vi đường đua:

\(C=2\pi R=2\pi\) (km)

Khoảng cách giữa các trạm (tính theo độ dài cung tròn, không phải theo đường chim bay):

\(\frac{2\pi}{3}\) (km) \(\approx2,094\left(km\right)\)