Cho hình chữ nhật ABCD xó AB = 3cm, AC= 4cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD.
a) Chứng minh ∆ABH ~ ∆ACD
b) Tính độ dài đoạn thẳng DH
c) Gọi M,N theo thứ tự là các điểm thuộc các đoạn BH, CD sao cho BM= 1/2 MH, CN = 1/3CD. Chứng minh ∆ABM~∆ACN. Từ đó suy ra AM vuông góc MN
Mấy anh chị lớn hơn 2k5 and mấy bạn 2k5 ai giải được bài này thì giúp mình vs mình sắp thi r. Thank all


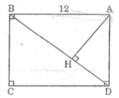
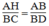
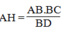
a) Xét \(\Delta ABH\) và \(\Delta ACD\) có :
\(\widehat{AHB}=\widehat{BCD}=90^o;\widehat{ABD}=\widehat{CDB}\) ( cùng phụ với \(\widehat{CBD}\) )
\(\Rightarrow\) \(\Delta ABH\) ~ \(\Delta ACD\)
\(\Rightarrow\) \(\frac{AB}{AC}=\frac{BH}{CD}\)
b) Có \(\frac{AB}{AC}=\frac{BH}{CD}\Rightarrow BH=\frac{AB.CD}{AC}=2.25cm\)
Vì Tứ giác ABCD là hình chữ nhât \(\Rightarrow\) BD = AC = 4cm
Có BH + DH = BD \(\Rightarrow\) DH = 1,75 cm
c) Có : \(\frac{BM}{MN}=\frac{1}{2}\Rightarrow BM=\frac{1}{3}BH\) (1)
Lại có: \(\frac{BH}{CD}=\frac{2,25}{3}\Rightarrow BH=\frac{3}{4}CD\) (2)
Từ (1) và (2) \(\Rightarrow BM=\frac{1}{4}CD\)(3 )
Có \(CN=\frac{1}{3}CD\Rightarrow CD=3CN\) (4)
Từ (3) và (4) \(\Rightarrow\frac{BM}{CN}=\frac{3}{4}\)
Có \(\frac{AB}{AC}=\frac{3}{4}\)
Gọi I là giao điểm của 2 đường chéo AC và BD
=> DI = CI \(\Rightarrow\Delta DIC\) cân tại I \(\Rightarrow\widehat{IDC}=\widehat{ICD}\)
mà \(\widehat{ABD}=\widehat{CDB}\)
\(\Rightarrow\widehat{ICD}=\widehat{ABD}hay\widehat{ACN}=\widehat{ABM}\)
Xét \(\Delta ABM\) và \(\Delta ACN\) có:
\(\frac{BM}{CN}\)\(=\frac{AB}{AC}=\frac{3}{4}\) ; \(\widehat{ABD}=\widehat{ACD}\)
\(\Rightarrow\) \(\Delta ABM\) ~ \(\Delta ACN\)
\(\Rightarrow\) \(\frac{AM}{AN}=\frac{AB}{AC}\Leftrightarrow\frac{AM}{AB}=\frac{AN}{AC}\) ( 5 )và \(\widehat{BAM}=\widehat{CAN}\)
Có \(\widehat{ABM}+\widehat{MAC}=\widehat{BAC}\) ; \(\widehat{MAC}=\widehat{CAN}=\widehat{MAN}\)
mà \(\widehat{BAM}=\widehat{CAN}\) \(\Rightarrow\) \(\widehat{BAC}=\widehat{MAN}\) ( 6 )
Từ (5) và (6) \(\Rightarrow\Delta AMN\sim\Delta ABC\Rightarrow\widehat{AMN}=\widehat{ABC}=90^o\) hay \(AM\perp MN\) (đpcm)
Câu a,b k cần làm cx được nhé