Biết rằng hai đường thẳng vuông góc với nhau khi tích hai hệ số góc của chúng bằng -1.
Đường thẳng có phương trình y=ax+by=ax+b vuông góc với đường thẳng y=\frac{-1}{4}x+0y=4−1x+0 và đi qua điểm C(1,4)C(1,4).
a= ?
b =?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=ax+b\left(d\right);y=-\dfrac{1}{2}x+\dfrac{1}{2}\left(d'\right)\)
\(\left(d\right)\perp\left(d'\right)\Leftrightarrow-\dfrac{1}{2}a=-1\Leftrightarrow a=2\Rightarrow y=2x+b\left(d\right)\)
Lại có \(\left(d\right)\) đi qua \(A\left(-1;2\right)\Rightarrow2=-2+b\Rightarrow b=4\)
\(\Rightarrow y=2x+4\left(d\right)\)

Đồ thị hàm số vuông góc với đường thẳng y = 4x + 1 nên 4.a = -1 hay 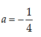
Đồ thị hàm số đi qua điểm N(4; -1) nên -1 = a.4 + b hay b = 0
Suy ra P = ab = 0
Chọn A.

1: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-2\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=1-2a=1-2\cdot\left(-3\right)=7\end{matrix}\right.\)
2: Vì (d)//y=-3x+2 nên a=-3
Vậy: y=-3x+b
Thay x=3 và y=3 vào y=-3x+b, ta được:
b-9=3
hay b=12

a) \({d_1}\) song song với đường thẳng \({d_2}:x + 3y + 2 = 0\) nên nhận vectơ pháp tuyến của đường thẳng \({d_2}\) làm vectơ pháp tuyến là \(\overrightarrow n = \left( {1;3} \right)\)
\({d_1}\) đi qua điểm \(A(2;3)\) nên ta có phương trình tổng quát
\(\left( {x - 2} \right) + 3.\left( {y - 3} \right) = 0 \Leftrightarrow x + 3y - 11 = 0\)
b) \({d_1}\) vuông góc với đường thẳng \({d_3}:3x - y + 1 = 0\) nên nhận vectơ pháp tuyến của đường thẳng \({d_3}\) làm vectơ chỉ phương là \(\overrightarrow u = \left( {3; - 1} \right)\)
\({d_1}\) đi qua điểm \(B(4; - 1)\) nên ta có phương trình tham số: \(\left\{ \begin{array}{l}x = 4 + 3t\\y = - 1 - t\end{array} \right.\)