Question

[Vũ Quang Minh]

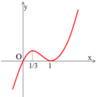
Cho hàm số f(x) có đạo hàm f'(x) = (x-1)²(x²-2x) với mọi x ∈ R. Có bao nhiêu số nguyên m < 100 để hàm số g(x) = f(x²-8x+m) đồng biến trên khoảng (4;+∞) ?
A. 18
B. 82
C. 83
D. 84

Answer 1

[Nguyễn Việt Lâm]

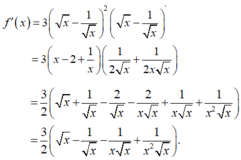
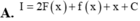
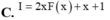
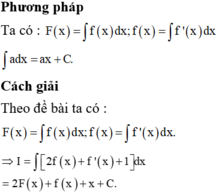
\(g'\left(x\right)=\left(2x-8\right)f'\left(x^2-8x+m\right)\)

Ta không cần quan tâm tới nhân tử \(\left(x-1\right)^2\) ở \(f'\left(x\right)\) vì đó là biểu thức mũ chẵn nên ko làm \(f'\left(x\right)\) đổi dấu khi đi qua \(x=1\)

\(g'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}2x-8=0\Rightarrow x=4\\\left(x^2-8x+m\right)^2-2\left(x^2-8x+m\right)=0\left(1\right)\end{matrix}\right.\)

Để hàm số đồng biến trên \(\left(4;+\infty\right)\Rightarrow\left(1\right)\) vô nghiệm hoặc tất cả các nghiệm của (1) đều không lớn hơn 4

\(\left(1\right)\Leftrightarrow\left(x^2-8x+m\right)\left(x^2-8x+m-2\right)=0\)

TH1: \(16-m+2\le0\Rightarrow m\ge18\)

TH2: Nhận thấy 2 pt \(\left\{{}\begin{matrix}x^2-8x+m=0\\x^2-8m+m-2=0\end{matrix}\right.\)

Đều có trung bình cộng hai nghiệm \(\frac{x_1+x_2}{2}=4\Rightarrow\) nếu 2 pt này có nghiệm thì luôn có ít nhất 1 nghiệm lớn hơn 4 \(\Rightarrow\) ko thỏa mãn

Vậy \(m\ge18\) \(\Rightarrow\) có \(99-18+1=82\) giá trị nguyên của m

Answer 2

[Ý Phan Lê Như]

Vì sao ra 16-m+2=0 ạ