Cho hình thang ABCD vuông tại A,đáy nhỏ AB.Đường chéo DB vuông góc với cạnh bên BC tại B.Chứng minh rằng:
a)Hai tam giác ADB và BCD đồng dạng
b)\(\left(\frac{AD}{DB}\right)^2=\frac{AB}{CD}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 2 2023
a: góc ADB=90 độ-góc ABD
=góc CBD
b: Xét ΔABD vuông tại A và ΔBDC vuông tại B có
góc ABD=góc BDC
=>ΔABD đồng dạng vơi ΔBDC
15 tháng 6 2023
a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
góc E chung
=>ΔBDE đồng dạng với ΔDCE
b: BD=căn 8^2+6^2=10cm
BE=10^2/6=100/6=50/3cm
EC=DC^2/BC=8^2/6=32/3cm
Xét ΔEBD có CH//BD
nên CH/BD=EC/EB
=>CH/10=32/50=16/25
=>CH=160/25=6,4cm
CM
29 tháng 9 2017
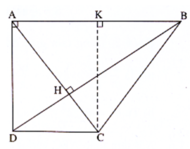
Hai đường chéo AC, BD cắt nhau tại H. Trong tam giác vuông ABD, ta có:
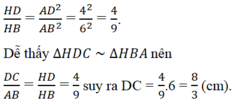
Kẻ đường cao CK của tam giác ABC, dễ thấy KB = AB – DC = 6 - 8/3 = 10/3.
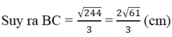
Tam giác vuông ABD có D B 2 = A B 2 + A D 2 = 6 2 + 4 2 = 52, từ đó DB = 52 = 2 13 (cm)
LN
19 tháng 4 2019
Gọi r là chiều rộng
d là chiều dài
Chu vi hình vuông là:
9.4=36( cm)
=> chu vi hình vuông là 36 cm
=>( r+d).2=36( cm)
=>( r+d)=18( cm)
=> r=8(cm)
Vậy chiều rộng hình chữ nhật là 8cm