Giúp mik làm 3 câu này nha ( Toán hình ) :
1. Cho tam giác ABC. Hãy viết kết luận của hai bài toán sau về quan hệ giữa góc và cạnh đối diện trong một tam giác
| Bài Toán 1 | Bài Toán 2 | |
| Giả Thiết | AB > AC | góc B < góc C |
| Kết luận |
2. Từ điểm A không thuộc đường thẳng d , kẻ đường vuông góc AH , các đường xiên AB , AC đến đườn thẳng d . Hãy điền dấu ( < , > ) vào các chỗ trống ( ... ) dưới đây cho đúng :
a) AB....... AH ; AC...... AH
b) Nếu HB..... HC thì AB.......AC
c) Nếu AB..... AC thì HB..... HC
3.Cho tam giác DEF . Hãy viết các bất đẳng thức về quan hệ giữa các cạnh của tam giác này.
*Giúp mik nha , ai trl thì đc tick nha , ai cũng đc nhưng phải trl 1 trong 3 câu trên
~Mino~





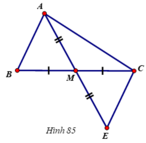
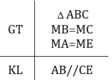
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có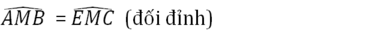

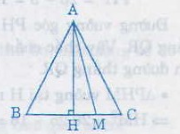
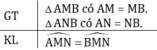
Câu 1
Kết luận góc C < góc B
Kết luận AC < AB
Câu 2:
a) AB>AH ; AC>AH
b) HB<HC thì AB<AC
c) Nếu AB<AC thì HB<HC
Câu 3
\(|DE-DF|̀< EF< DE+DF\)
\(|DE-EF|< DF< DE+EF\)
\(|DF-EF|< DE< DF+EF\)
thank u so much , bro :))))