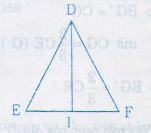
Cho tam giác DEF cân tại D với đường trung tuyến DI.
a) Chứng minh ΔDEI = ΔDFI.
b) Các góc DIE và góc DIF là những góc gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 4 2022
xét ΔDIE và ΔDIF có :
\(DB=DE\left(gt\right)\\ \widehat{DEI}=\widehat{DFI}\left(tgD\text{EF}c\text{â}nt\text{ại}D\right)\\ DI:chung\)
=> ΔDIE = ΔDIF (c.g.c )
=> góc DIE = góc DFI ( 2 góc t.ư)
có tg DEF cân tại D , đường trung tuyến DI
=> DI là đường trung trực
=> \(\widehat{DIE}=\widehat{D\text{IF}}=\dfrac{180^O}{2}=90^O\)
=> 2 GÓC là góc vuông
C) có tg DIE = tg DIF (cmt)
=> EI = FI ( 2 CẠNH t/ư)
=> EI = FI =1/2EF = 10:2 = 5 cm
có DEI là tg vuông tại I ( I là đường trung trực của tg DEF )
ADĐL P-T-G vào tg vuông DIE ta có
\(EI^2+ID^2=DE^2\\
\Leftrightarrow DE^2=12^2+5^2\\
\Leftrightarrow DE^2=169\\
\Leftrightarrow DE=13cm\)
TT
18 tháng 4 2022
cho tam giác ABC vuông ở A, có góc C=30 độ AH vuông góc với BC.( H thuộc BC) .Trên đoạn HC lấy điểm D sao cho HD=HB. từ C kẽ CE vuông với AD. chứng minh rằng:
A. tam giác ABD là tam giác đều
B. AH=CE
C. EH//AC
giúp mik với mik đg cần gấp
27 tháng 4 2021
XÉT tam giác ΔDEI và ΔDFI có:
DE = DF (TAM GIÁC CÂN)
EI = FI (ĐƯỜNG TRUNG TUYẾN)
DI LÀ CẠNH CHUNG
==> ΔDEI = ΔDFI ( C.G.C )
11 tháng 8 2021
a: Xét ΔDEI và ΔDFI có
DE=DF
DI chung
IE=IF
Do đó: ΔDEI=ΔDFI
b: Ta có: ΔDEI=ΔDFI
nên \(\widehat{DIE}=\widehat{DIF}\)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)
nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)
11 tháng 8 2021
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
b) Vì ∆DEI = ∆DFI =>
mà = 1800 ( kề bù)
nên = 900
PT
11 tháng 4 2021
a) Xét ΔDEI và ΔDFI c
DE = DF (ΔDEF cân)
DI là cạnh chung.
IE = IF (DI là trung tuyến)
➩ ΔDEI = ΔDFI (c.c.c)
b) Vì ∆DEI = ∆DFI => \(\widehat{DIE}\) \(= \widehat{DIF}\)
mà \(\widehat{DIE}\)+\(\widehat{DIF}\)=1800( kề bù)
nên \(\widehat{DIE}\)\(= \widehat{DIF}\)=900
c) I là trung điểm của EF nên IE = IF = 5cm.
ΔDIE vuông tại I
➩ DE2=DI2+EI2 (định lí Pitago)
➩ DI2=132–52=144
➩DI=12.
25 tháng 6 2023
a: Xét ΔDEI và ΔDFI có
DE=DF
EI=FI
DI chung
=>ΔDEI=ΔDFI
b: ΔDEI=ΔDFI
=>góc DIE=góc DIF=180/2=90 độ
=>góc DIE và góc DIF là những góc vuông
c: EI=FI=10/2=5cm
=>DE=căn 5^2+12^2=13cm
8 tháng 4 2015
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
b) Vì ∆DEI = ∆DFI =>
mà = 1800 ( kề bù)
nên = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
1 đúng nhé
5 tháng 8 2017
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
b) Vì ∆DEI = ∆DFI =>
mà = 1800 ( kề bù)
nên = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
13 tháng 5 2019
a/ xét /\ DEF cân tại D
=> DE = DF (t/c /\ cân )
DI là trung tuyến
=> DI vuông với FE => DIE = 90* => DIF kề bù với DIE => DIF = 90* (1)
=> I là trung điểm EF
Xét /\ DIF và /\ DIE có :
DIF = DIE (cmt )
DF =DE (cmt)
IF = IE ( cmt )
=> /\ DIE = /\ DIF (c.g.c)
b/ (1) => DIE = DIF = 90*
=> 2 góc này là hai góc vuông
c/ chịu .
ko cần vẽ hình và viết giả thiết kết luận đâu nhé
còn có câu c là
c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.